3x + 2 > x - 4 এর সমাধান-
A
(- ∞, - 3)
B
(- 3, ∞)
C
(3, ∞)
D
(- ∞, 3)
উত্তরের বিবরণ
প্রশ্ন: 3x + 2 > x - 4 এর সমাধান-
সমাধান:
3x + 2 > x - 4
⇒ 3x - x > - 4 - 2
⇒ 2x > - 6
⇒ x > - 3
সুতরাং, নির্ণেয় সমাধান সেট হলো (- 3, ∞)।
(- 3, ∞) বলতে বোঝায় যে, - 3 এর চেয়ে বড় সব বাস্তব সংখ্যা এই সমাধানের অন্তর্ভুক্ত।
0
Updated: 1 month ago
a এর মান কত হলে 4x2 + 20x + a রাশিটি একটি পূর্ণবর্গ হবে?
Created: 1 month ago
A
16
B
20
C
24
D
25
প্রশ্ন: a এর মান কত হলে 4x2 + 20x + a রাশিটি একটি পূর্ণবর্গ হবে?
সমাধান:
4x2 + 20x + a রাশিটি পূর্ণবর্গ হবে যদি এটি (2x + 5)2 আকারের হয়।
(2x + 5)2 = (2x)2 + 2 × (2x) × 5 + 52
= 4x2 + 20x + 25
প্রদত্ত রাশি 4x2 + 20x + a এর সাথে তুলনা করে পাই,
a = 25
∴ a এর মান 25 হলে প্রদত্ত রাশিটি একটি পূর্ণবর্গ হবে।
0
Updated: 1 month ago
এর মান কত?
Created: 2 months ago
A
0
B
1
C
1/2
D
a(m + n)
গণিত
বীজগণিত (Algebra)
বীজগণিতীয় রাশিমালা (Algebraic expressions)
বীজগণিতীয় রাশিমালার যোগ, বিয়োগ, গুণ ও ভাগ (Addition, subtraction, multiplication and division of algebraic expressions)
সূচক (Exponents /Indices)
প্রশ্ন: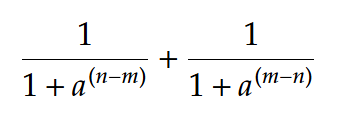 
এর মান কত?
সমাধান:
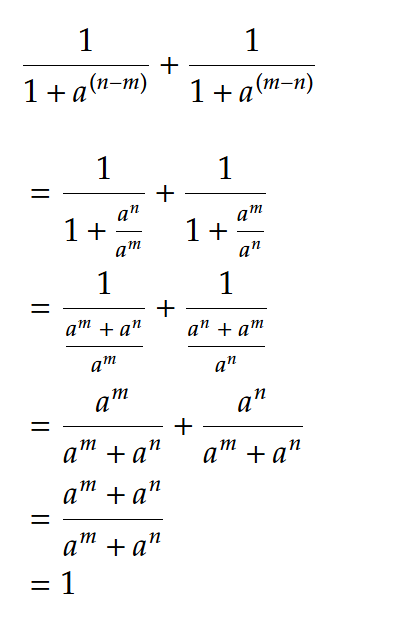
0
Updated: 2 months ago
If 3x2 + 14x + 8 is divided by x + 4, the result is:
Created: 3 weeks ago
A
3x + 2
B
2x - 3
C
5x + 1
D
2x + 3
3x2 + 14x + 8
= 3x2 + 12x + 2x + 8
= 3x(x + 4) + 2(x + 4)
= (x + 4)(3x + 2)
এখন,
(3x2 + 14x + 8)/(x + 4)
= (x + 4)(3x + 2)/(x + 4)
= 3x + 2
সুতরাং, ভাগফল হলো 3x + 2।
0
Updated: 3 weeks ago
