(x + 2y, 7) = (16, x - y) হলে (x, y) = কত?
A
(10, 3)
B
(- 2, - 4)
C
(4, 5)
D
(1, 5)
উত্তরের বিবরণ
প্রশ্ন: (x + 2y, 7) = (16, x - y) হলে (x, y) = কত?
সমাধান:
(x + 2y, 7) = (16, x - y) )
x + 2y = 16 ..................(1)
এবং, x - y = 7 ...........(2)
(1) নং থেকে (2) নং বিয়োগ করে পাই,
x + 2y - x + y = 16 - 7
⇒ 3y = 9
∴ y = 3
y এর মান (1) নং এ বসিয়ে পাই,
x + 2. 3 = 16
⇒ x + 6 = 16
⇒ x = 16 - 6
∴ x = 10
সুতরাং, নির্ণেয় সমাধান: (x, y) = (10, 3)
0
Updated: 5 months ago
Created: 5 months ago
A
224
B
180
C
204
D
302
প্রশ্ন:
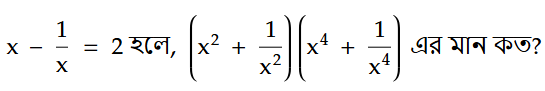
সমাধান:
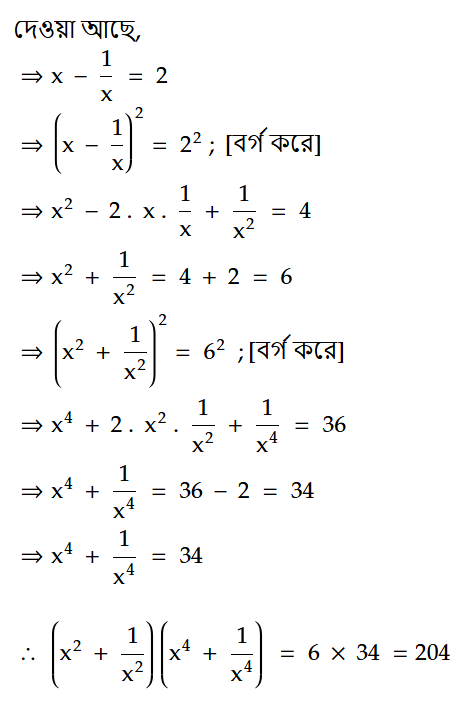
0
Updated: 5 months ago
যদি a + b = 5 এবং a2 + b2 = 13 হয়, তবে a3 + b3 এর মান কত?
Created: 1 month ago
A
28
B
35
C
65
D
81
প্রশ্ন: যদি a + b = 5 এবং a2 + b2 = 13 হয়, তবে a3 + b3 এর মান কত?
সমাধান:
দেয়া আছে, a + b = 5 এবং a2 + b2 = 13
এখন,
(a + b)2 = a2 + b2 + 2ab
⇒ 52 = 13 + 2ab
⇒ 25 = 13 + 2ab
⇒ 25 - 13 = 2ab
⇒ 12 = 2ab
⇒ ab = 6
∴ a3 + b3 = (a + b)3 - 3ab(a + b)
⇒ a3 + b3 = (5)3 - 3(6)(5)
⇒ a3 + b3 = 125 - 90
∴ a3 + b3 = 35
0
Updated: 1 month ago
যদি x + (1/x) = 4 হয়, তাহলে x4 + (1/x4) এর মান কত?
Created: 1 month ago
A
196
B
194
C
198
D
256
প্রশ্ন: যদি x + (1/x) = 4 হয়, তাহলে x4 + (1/x4) এর মান কত?
সমাধান:
দেওয়া আছে,
x + (1/x) = 4
⇒ (x + 1/x)2 = 42 [উভয় পাশে বর্গ করে]
⇒ x2 + 2 × x × (1/x) + 1/x2 = 16
⇒ x2 + (1/x2) = 16 - 2
⇒ x2 + (1/x2) = 14
আবার,
⇒ {x2 + (1/x2)}2 = 142
⇒ (x2)2 + 2 × x2 × (1/x2) + (1/x2)2 = 196
⇒ x4 + 2 + (1/x4) = 196
⇒ x4 + (1/x4) = 196 - 2
∴ x4 + (1/x4) = 194
0
Updated: 1 month ago