একটি সমবাহু ষড়ভুজের অভ্যন্তরে অঙ্কিত বৃহত্তম বৃত্তের আয়তন 100π হলে ঐ ষড়ভুজের আয়তন কত?
A
200
B
200√2
C
200√3
D
200√5
উত্তরের বিবরণ
প্রশ্ন: একটি সমবাহু ষড়ভুজের অভ্যন্তরে অঙ্কিত বৃহত্তম বৃত্তের ক্ষেত্রফল 144π হলে ঐ ষড়ভুজের ক্ষেত্রফল কত?
সমাধান:
বৃত্তের ক্ষেত্রফল πr2 = 100π
r2 = 100
r2 = 102
r = 10
ষড়ভুজের ভিতর 6টি সমবাহু ত্রিভুজের শীর্ষের ছেদ বিন্দু বৃত্তটির কেন্দ্রে অবস্থিত।
6টি ত্রিভুজের ক্ষেত্রফলের সমষ্টি হবে ষড়ভুজটির ক্ষেত্রফল।
এখানে
(√3/4) × a2 = (1/2) × a × 10
(√3/4) × a2 = 5a
a = 20/√3
ষড়ভুজের ক্ষেত্রফল = 6 × (√3/4) × (20/√3) × (20/√3)
= 200√3
0
Updated: 5 months ago
ABC ত্রিভুজে AB = 8 মিটার, BC = 10 মিটার এবং ক্ষেত্রফল 20√3 বর্গমিটার হলে, ∠B = ?
Created: 1 month ago
A
30°
B
60°
C
90°
D
45°
প্রশ্ন: ABC ত্রিভুজে AB = 8 মিটার, BC = 10 মিটার এবং ক্ষেত্রফল 20√3 বর্গমিটার হলে, ∠B = ?
সমাধান:
দেওয়া আছে,
AB = 8 মিটার
BC = 10 মিটার
এবং ABC ত্রিভুজে ক্ষেত্রফল = 20√3 বর্গমিটার
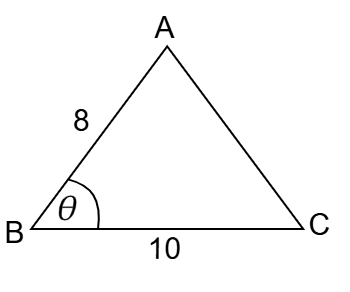
আমরা জানি,
একটি ত্রিভুজের সন্নিহিত বাহুদ্বয় a, b হলে এবং তাদের অন্তর্ভুক্ত কোণ θ হলে,
ক্ষেত্রফল = (1/2)ab sinθ
∴ ত্রিভুজ ABC এর ক্ষেত্রফল = (1/2) × AB × BC × sinθ
⇒ 20√3 = (1/2) × 8 × 10 × sin ∠B
⇒ 20√3 = 40 × sin ∠B
⇒ sin ∠B = 20√3/40
⇒ sin ∠B = √3/2
⇒ sin ∠B = sin 60°
⇒ ∠B = 60°
0
Updated: 1 month ago
ত্রিভুজের তিনটি বাহুর লম্ব সমদ্বিখণ্ডকগুলো যে বিন্দুতে ছেদ করে, তাকে কী বলা হয়?
Created: 1 month ago
A
অন্তঃকেন্দ্র
B
ভরকেন্দ্র
C
বহিঃকেন্দ্র
D
পরিকেন্দ্র
প্রশ্ন: ত্রিভুজের তিনটি বাহুর লম্ব সমদ্বিখণ্ডকগুলো যে বিন্দুতে ছেদ করে, তাকে কী বলা হয়?
সমাধান:
• পরিকেন্দ্র (Circumcentre): ত্রিভুজের তিনটি বাহুর লম্ব সমদ্বিখণ্ডকগুলো যে বিন্দুতে ছেদ করে, তাকে পরিকেন্দ্র বলা হয়।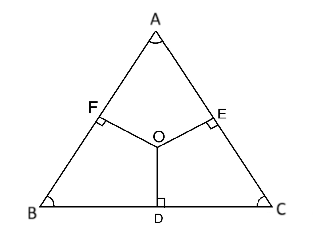
চিত্রে O বিন্দুটি হলো পরিকেন্দ্র (Circumcentre)।
উল্লেখ্য,
• অন্তঃকেন্দ্র: ত্রিভুজের তিন কোণের সমদ্বিখণ্ডকগুলো যে বিন্দুতে ছেদ করে তাকে অন্তঃকেন্দ্র বলে।
• ভরকেন্দ্র: ত্রিভুজের মধ্যমাগুলোর ছেদবিন্দুকে ভরকেন্দ্র বলে।
• বহিঃকেন্দ্র: একটি ত্রিভুজের একটি অন্তঃস্থ কোণের সমদ্বিখণ্ডক এবং অপর দুটি বহিঃস্থ কোণের সমদ্বিখণ্ডক যে বিন্দুতে ছেদ করে, তাকে বহিঃকেন্দ্র বলে।
0
Updated: 1 month ago
কোনো ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি কত হবে?
Created: 2 months ago
A
১৪০°
B
১৮০°
C
৩৬০°
D
৫৪০°
গণিত
ঘন জ্যামিতি (Solid geometry)
জ্যামিতি (geometry)
জ্যামিতি প্রাথমিক ধারণা (Basic Concept)
ত্রিভুজ (Triangle)
সমাধান:
আমরা জানি,
ত্রিভুজের কোনো এক বাহুকে বর্ধিত করলে একবাহুতে সৃষ্ট কোণ = অন্তঃস্থ কোণ + বহিঃস্থ কোণ = ১৮০°
তিনটি বাহুকে বর্ধিত করলে উৎপন্ন কোণ = ৩ × (অন্তঃস্থ কোণ + বহিঃস্থ কোণ) = ৩ × ১৮০° = ৫৪০°
আবার, আমরা জানি ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি = ১৮০°
প্রশ্নমতে,
৩ টি বহিঃস্থ কোণ + ৩ টি অন্তঃস্থ কোণ = ৫৪০°
⇒ ৩ টি বহিঃস্থ কোণ + ১৮০° = ৫৪০°
⇒ ৩ টি বহিঃস্থ কোণ = ৫৪০° - ১৮০° = ৩৬০°
সুতরাং, বহিঃস্থ কোণ তিনটির সমষ্টি = ৩৬০°
0
Updated: 2 months ago