A
3, 5, 8
B
3, 5, 6
C
3, 4, 5
D
3, 6, 9
উত্তরের বিবরণ
প্রশ্ন: নিচের কোন তিনটি রেখাংশের দৈর্ঘ্য দ্বারা একটি সমকোণী ত্রিভুজ আঁকা সম্ভব?
সমাধান:
পীথাগোরাসের উপপাদ্য অনুসারে,
একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।
∴ 32 + 42 = 52
বা, 9 + 16 = 25
0
Updated: 6 days ago
একটি সমবাহু ত্রিভুজের শীর্ষবিন্দু থেকে ভর কেন্দ্রের দূরত্ব 14 সে.মি. হলে ত্রিভুজটির মধ্যমা কত?
Created: 1 week ago
A
18 সে.মি.
B
20 সে.মি.
C
21 সে.মি.
D
24 সে.মি.
প্রশ্ন: একটি সমবাহু ত্রিভুজের শীর্ষবিন্দু থেকে ভর কেন্দ্রের দূরত্ব 14 সে.মি. হলে ত্রিভুজটির মধ্যমা কত?
সমাধান:
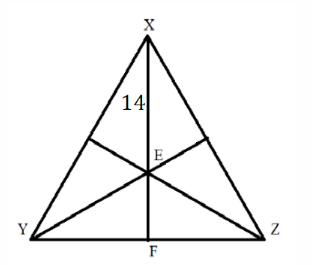
আমরা জানি
ত্রিভুজের মধ্যমাত্রয় যে বিন্দুতে মিলিত হয় সেই বিন্দুকে ঐ ত্রিভুজের ভরকেন্দ্র বলে।
∴ EX : EF = 2 : 1
⇒ 14 : EF = 2 : 1
⇒ 14/EF = 2/1
⇒ 2EF = 14
⇒ EF = 14/2
⇒ EF = 7
∴ ত্রিভুজটির মধ্যমা = FX = EX + EF = 14 + 7 = 21 সে.মি.
0
Updated: 1 week ago
৪ সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের অন্তঃস্থ একটি সমবাহু ত্রিভুজের ক্ষেত্রফল কত হবে?
Created: 3 days ago
A
২√৩ বর্গ সে.মি.
B
√৩/২ বর্গ সে.মি.
C
১২√৩ বর্গ সে.মি.
D
২১√২ বর্গ সে.মি.
প্রশ্ন: ৪ সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের অন্তঃস্থ একটি সমবাহু ত্রিভুজের ক্ষেত্রফল কত হবে?
সমাধান:
দেওয়া আছে,
বৃত্তের ব্যাসার্ধ = ৪ সে.মি.
আমরা জানি,
বৃত্তের অন্তঃস্থ সমবাহু ত্রিভুজের বাহু = √৩ × বৃত্তের ব্যাসার্ধ
= √৩ × ৪
= ৪√৩
এখন,
সমবাহু ত্রিভুজের ক্ষেত্রফল = (√৩/৪) × (বাহু)২
= (√৩/৪) × (৪√৩)২
= (√৩/৪) × ১৬ × ৩
= ১২√৩
∴ সমবাহু ত্রিভুজের ক্ষেত্রফল = ১২√৩ বর্গ সে.মি.
0
Updated: 3 days ago
ABC সমদ্বিবাহু ত্রিভুজের ∠C = 90° , AC = 5 সে.মি. হলে AB = ?
Created: 1 week ago
A
25
B
7√2
C
5
D
5√2
প্রশ্ন: ABC সমদ্বিবাহু ত্রিভুজের ∠C = 90° , AC = 5 সে.মি. হলে AB = ?
সমাধান:
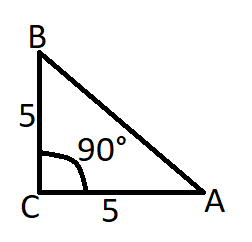
দেওয়া আছে,
ABC সমদ্বিবাহু ত্রিভুজে,
∠C = 90°
AC = 5 সে.মি.
∴ AC = BC = 5 সে.মি.
মনে করি,
ABC সমদ্বিবাহু সমকোণী ত্রিভুজে, AC = ভূমি, BC = লম্ব, AB = অতিভুজ
পিথাগোরাসের উপপাদ্য অনুযায়ী,
AB2 = BC2 + AC2
⇒ AB2 = 52 + 52
⇒ AB2 = 25 + 25
⇒ AB2 = 50
⇒ AB = √50
⇒ AB = √(25 × 2)
⇒ AB = 5√2
0
Updated: 1 week ago