ΔABC ত্রিভুজের ∠B এর পরিমাণ ৫২° এবং AB = AC হয়, তাহলে ∠A এর মান কত
A
৮৪°
B
৬৬°
C
৭৬°
D
৭৮°
উত্তরের বিবরণ
প্রশ্ন: ΔABC ত্রিভুজের ∠B এর পরিমাণ ৫২° এবং AB = AC হয়, তাহলে ∠A এর মান কত?
সমাধান:
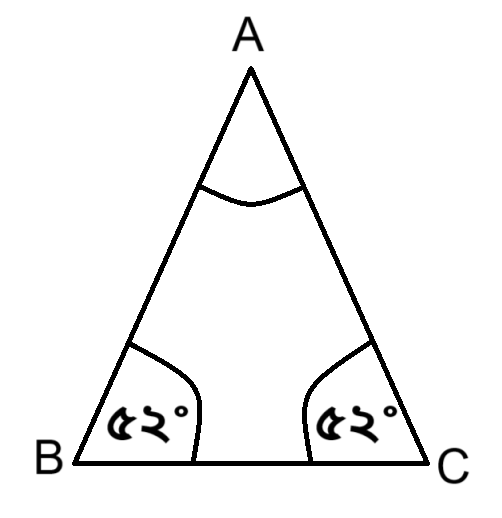
চিত্রে, ∠B = ৫২° এবং AB = AC
∴ ∠B = ∠C = ৫২°
আমরা জানি,
ত্রিভুজের তিনটি কোণের সমষ্টি ১৮০°
প্রশ্নমতে,
⇒ ∠A + ∠B + ∠C = ১৮০°
⇒ ∠A + ৫২° + ৫২° = ১৮০°
⇒ ∠A + ১০৪° = ১৮০°
⇒ ∠A = ১৮০° - ১০৪° = ৭৬°
∴ ∠A = ৭৬°
0
Updated: 1 month ago
If p is the circumference of the circle Q and the area of the circle is 25π, what is the value of p?
Created: 3 weeks ago
A
25
B
10π
C
35
D
25π
Question: If p is the circumference of the circle Q and the area of the circle is 25π, what is the value of p?
Solution:
বৃত্তের ক্ষেত্রফল (A) = πr2
প্রশ্নানুসারে, বৃত্তের ক্ষেত্রফল 25π।
∴ πr2 = 25π
⇒ r2= 25
⇒ r = √25
⇒ r = 5
সুতরাং, বৃত্তের ব্যাসার্ধ (r) হলো 5।
এখন, বৃত্তের পরিধি (p) = 2πr
∴ p = 2π(5)
⇒ p = 10π
সুতরাং p-এর মান 10π
0
Updated: 3 weeks ago
ΔABC সমবাহু ত্রিভুজের একটি মধ্যমা AD এবং G ভরকেন্দ্র। GD = ৫ সেমি হলে AD = ?
Created: 1 week ago
A
১৫ সেমি
B
১০ সেমি
C
৭.৫ সেমি
D
১২ সেমি
প্রশ্ন: ΔABC সমবাহু ত্রিভুজের একটি মধ্যমা AD এবং G ভরকেন্দ্র। GD = ৫ সেমি হলে AD = ?
সমাধান:
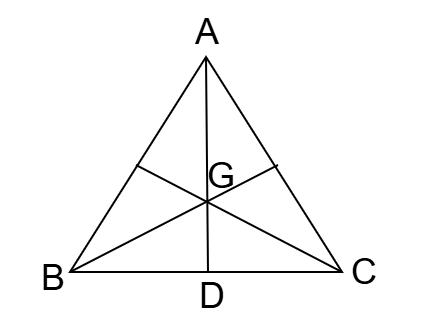
আমরা জানি,
ত্রিভুজের ভরকেন্দ্র (G) মধ্যমাকে (AD) ২ : ১ অনুপাতে বিভক্ত করে।
অর্থাৎ, AG : GD = ২ : ১
দেওয়া আছে, GD = ৫ সেমি।
প্রশ্নমতে,
AG : GD = ২ : ১
⇒ AG/৫ = ২/১
⇒ AG = ৫ × ২
∴ AG = ১০
এখন, মধ্যমা AD = AG + GD
= ১০ সেমি + ৫ সেমি
= ১৫ সেমি
0
Updated: 1 week ago
ত্রিভুজের বাহুত্রয়ের লম্ব সমদ্বিখণ্ডকের তিনটি ছেদবিন্দু হলো -
Created: 5 months ago
A
লম্বকেন্দ্র
B
অন্তকেন্দ্র
C
পরিকেন্দ্র
D
ভরকেন্দ্র
- লম্ব সমদ্বিখণ্ডক মানে কোনো বাহুকে সমান দুই ভাগে বিভক্ত করে এবং বাহুর উপর লম্ব থাকে।
- তিনটি বাহুর লম্ব সমদ্বিখণ্ডক যেখানে মিলিত হয়, সেটি হলো পরিকেন্দ্র।
- পরিকেন্দ্র হলো এমন একটি বিন্দু, যা ত্রিভুজের সব কোণের থেকে সমান দূরত্বে থাকে, এবং যেখান থেকে ত্রিভুজের একটি পরিঘর্ণবৃত্ত (circumcircle) আঁকা যায়।
সঠিক উত্তর: গ. পরিকেন্দ্র
0
Updated: 5 months ago