একটি সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য লম্ব অপেক্ষা 1 মিটার কম এবং লম্ব অপেক্ষা অতিভুজের দৈর্ঘ্য 1 মিটার বেশি হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত?
A
3 মিটার
B
4 মিটার
C
5 মিটার
D
6 মিটার
উত্তরের বিবরণ
প্রশ্ন: একটি সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য লম্ব অপেক্ষা 1 মিটার কম এবং লম্ব অপেক্ষা অতিভুজের দৈর্ঘ্য 1 মিটার বেশি হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত?
সমাধান:
ধরি,
সমকোণী ত্রিভুজের লম্বের দৈর্ঘ্য = x
∴ সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য = x - 1
∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = x + 1
আমরা জানি,
(অতিভুজ)2 = (লম্ব)2 + (ভূমি)2
⇒ (x + 1)2 = (x - 1)2 + x2
⇒ x2 + 2x + 1 = x2 - 2x + 1 + x2
⇒ x2 - 4x = 0
⇒ x(x - 4) = 0
⇒ x = 4 [যেহেতু, ত্রিভুজের লম্ব কখনো শূন্য হতে পারে না]
∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = (x + 1) মিটার
= (4 + 1) মিটার
= 5 মিটার ।
0
Updated: 1 month ago
কোনো ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি কত হবে?
Created: 2 months ago
A
১৪০°
B
১৮০°
C
৩৬০°
D
৫৪০°
গণিত
ঘন জ্যামিতি (Solid geometry)
জ্যামিতি (geometry)
জ্যামিতি প্রাথমিক ধারণা (Basic Concept)
ত্রিভুজ (Triangle)
সমাধান:
আমরা জানি,
ত্রিভুজের কোনো এক বাহুকে বর্ধিত করলে একবাহুতে সৃষ্ট কোণ = অন্তঃস্থ কোণ + বহিঃস্থ কোণ = ১৮০°
তিনটি বাহুকে বর্ধিত করলে উৎপন্ন কোণ = ৩ × (অন্তঃস্থ কোণ + বহিঃস্থ কোণ) = ৩ × ১৮০° = ৫৪০°
আবার, আমরা জানি ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি = ১৮০°
প্রশ্নমতে,
৩ টি বহিঃস্থ কোণ + ৩ টি অন্তঃস্থ কোণ = ৫৪০°
⇒ ৩ টি বহিঃস্থ কোণ + ১৮০° = ৫৪০°
⇒ ৩ টি বহিঃস্থ কোণ = ৫৪০° - ১৮০° = ৩৬০°
সুতরাং, বহিঃস্থ কোণ তিনটির সমষ্টি = ৩৬০°
0
Updated: 2 months ago
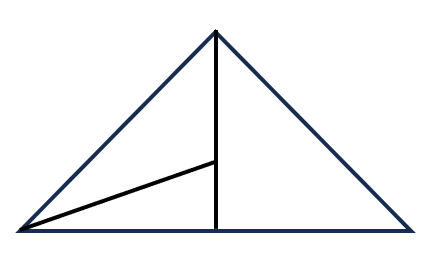
নিচের চিত্রে মোট কয়টি ত্রিভুজ আছে?
Created: 2 months ago
A
৪টি
B
৫টি
C
৬টি
D
৭টি
প্রশ্ন: নিচের চিত্রে মোট কয়টি ত্রিভুজ আছে?
সমাধান:
এখানে,
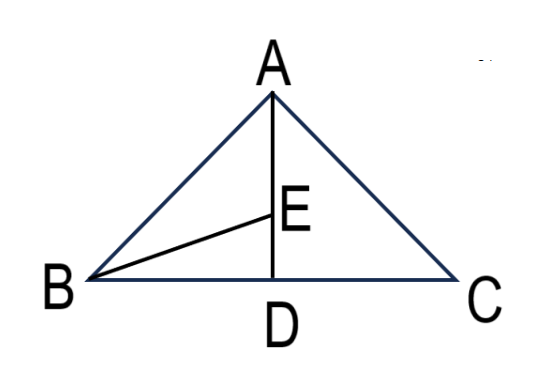
১টি ফাঁকা স্থান নিয়ে ত্রিভুজ আছে, ABE, BDE, ACD = ৩টি
২টি ফাঁকা স্থান নিয়ে ত্রিভুজ আছে, ABD = ১টি
৩টি ফাঁকা স্থান নিয়ে ত্রিভুজ আছে, ABC = ১টি
∴ মোট ত্রিভুজ আছে = ৩ + ১ + ১ = ৫টি
---------------------------------------
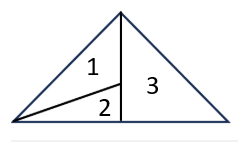
ত্রিভুজগুলো হলো: 1, 2, 3, 12, 123
∴ মোট ত্রিভুজ আছে = ৫টি
0
Updated: 2 months ago
The slope of a line perpendicular to one with slope (- 3/4) is:
Created: 3 weeks ago
A
4/3
B
3/4
C
1
D
- 4/3
Question: The slope of a line perpendicular to one with slope (- 3/4) is:
Solution:
আমরা জানি,
দুটি সরলরেখা পরস্পর লম্ব হলে তাদের ঢালদ্বয়ের গুণফল - 1 হয়।
অর্থাৎ, যদি কোনো সরলরেখার ঢাল (m) হয়, তাহলে তার উপর লম্ব রেখার ঢাল হবে - 1/m.
এখানে, মূল রেখার ঢাল = - 3/4 ।
তাই লম্ব রেখার ঢাল হবে = -1/(- 3/4) = 4/3
অতএব, লম্ব রেখার ঢাল = 4/3.
0
Updated: 3 weeks ago