5 সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র হতে 4 সে.মি. দূরবর্তী জ্যা এর দৈর্ঘ্য কত?
A
3 সে.মি.
B
4 সে.মি.
C
5.38 সে.মি.
D
6 সে.মি.
উত্তরের বিবরণ
প্রশ্ন: 5 সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র হতে 4 সে.মি. দূরবর্তী জ্যা এর দৈর্ঘ্য কত?
সমাধান:
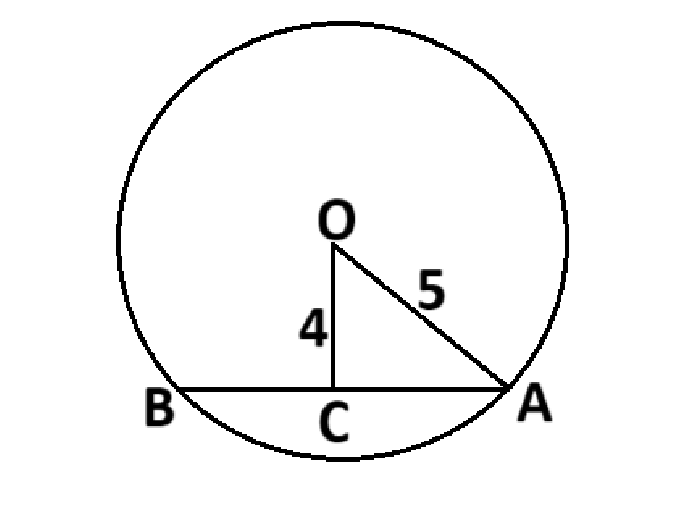
ধরি,
বৃত্তের কেন্দ্র O,
ব্যাসার্ধ = OA = 5 সে.মি.
O বিন্দু হতে AB জ্যা এর দূরত্ব = OC = 4 সে.মি.
OAC সমকোণী ত্রিভুজে,
পিথাগোরাসের উপপাদ্য অনুযায়ী,
OA2 = OC2 + AC2
⇒ AC2 = OA2 - OC2
⇒ AC2 = (5)2 - (4)2
⇒ AC2 = 25 - 16
⇒ AC2 = 9
⇒ AC = 3
C বিন্দু AB জ্যা কে সমদ্বিখণ্ডিত করে।
∴ AC = BC
∴ AB = AC + BC = AC + AC = 2AC
∴ AB = 2AC = (2 × 3) সে.মি. = 6 সে.মি.
0
Updated: 1 month ago
একটি সামান্তরিকের ভূমি উচ্চতার ৩/৪ অংশ এবং ক্ষেত্রফল ৪৩২ বর্গফুট হলে সামান্তরিকটির উচ্চতা কত?
Created: 2 months ago
A
১৮ ফুট
B
২৪ ফুট
C
৩৬ ফুট
D
৫২ ফুট
সমাধান:
ধরি,
সামান্তরিকের উচ্চতা = ৪ক ফুট
ভূমি = ৪ক × (৩/৪) = ৩ক ফুট
সামান্তরিকের ক্ষেত্রফল = ৪ক × ৩ক = ১২ক২
প্রশ্নমতে,
১২ক২ = ৪৩২
বা, ক২ = ৪৩২/১২
বা, ক২ = ৩৬
বা, ক = ৬
সুতরাং,
সামান্তরিকের উচ্চতা = (৪ × ৬) ফুট = ২৪ ফুট
0
Updated: 2 months ago
P সেটের প্রকৃত উপসেটের সংখ্যা 127 হলে, P সেটের উপাদান সংখ্যা কত?
Created: 1 month ago
A
10
B
9
C
8
D
7
প্রশ্ন: P সেটের প্রকৃত উপসেটের সংখ্যা 127 হলে, P সেটের উপাদান সংখ্যা কত?
সমাধান:
আমরা জানি,
উপাদানের সংখ্যা n হলে প্রকৃত উপসেট সংখ্যা = 2n - 1
প্রশ্নমতে,
2n -1 = 127
⇒ 2n = 127 + 1
⇒ 2n = 128
⇒ 2n = 27∴ n = 7
∴ P সেটের উপাদান সংখ্যা = 7
উপসেট: কোন সেটের উপাদান থেকে যতগুলো সেট গঠন করা যায় তাদের প্রত্যেকটি প্রদত্ত সেটের উপসেট। ফাঁকা সেট যে কোনো সেটের উপসেট।
প্রকৃত উপসেট: কোনো সেট থেকে গঠিত উপসেটের মধ্যে যে উপসেট গুলোর উপাদান সংখ্যা প্রদত্ত সেটের উপাদান সংখ্যা অপেক্ষা কম তাদেরকে প্রকৃত উপসেট বলে।
আমরা জানি,
উপাদানের সংখ্যা n হলে প্রকৃত উপসেট সংখ্যা = 2n - 1
2n -1 = 127
⇒ 2n = 127 + 1
⇒ 2n = 128
⇒ 2n = 27
0
Updated: 1 month ago
ত্রিভুজ ABC এর BE = FE = CF। AEC এর ক্ষেত্রফল ৪৮ বর্গফুট হলে, ত্রিভুজ ABC এর ক্ষেত্রফল কত বর্গফুট?
Created: 5 months ago
A
৭২
B
৬০
C
৪৮
D
৬৪
প্রশ্ন: ত্রিভুজ ABC এর BE = FE = CF। AEC এর ক্ষেত্রফল ৪৮ বর্গফুট হলে, ত্রিভুজ ABC এর ক্ষেত্রফল কত বর্গফুট?
সমাধান:
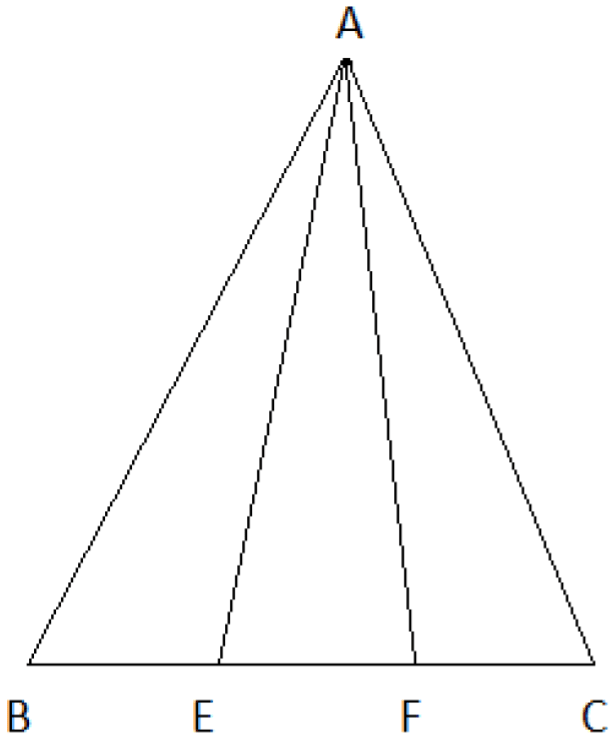
ত্রিভুজ AEC তে, EF = FC এবং AF মধ্যমা।
∴ ΔAEF = ΔAFC
আবার, ত্রিভুজ ABF তে, BE = EF এবং AE মধ্যমা।
∴ ΔABE = ΔAEF
∴ ΔABE = ΔAEF = ΔAFC
এখন,
ΔAEC = 48
⇒ ΔAEF + ΔAFC = 48
⇒ ΔAFC + ΔAFC = 48
⇒ 2.ΔAFC = 48
∴ ΔAFC = 24
∴ ΔABE = ΔAEF = ΔAFC = 24
সুতরাং,
ΔABC = ΔABE + ΔAEF + ΔAFC
= 24 + 24 + 24
= 72
0
Updated: 5 months ago