প্রশ্ন: একটি ঘড়ি প্রতিদিন ২০ মিনিট সময় হারায়। কতদিন পর ঘড়িটি এমন অবস্থায় পৌঁছাবে যখন ঘড়িটি সঠিক সময় নির্দেশ করবে? 

সমাধান: 
আমরা জানি,
ঘড়ির কাঁটার সম্পূর্ণ ঘন্টা = ১২ ঘন্টা
= ১২ × ৬০ মিনিট
= ৭২০ মিনিট সময় হারালে ঘড়িটি পুনরায় সঠিক সময় নির্দেশ করবে। 

এখন,
২০ মিনিট সময় হারায় = ১ দিনে
∴ ১ মিনিট সময় হারায় = ১/২০ দিনে
∴ ৭২০ মিনিট সময় হারায় = ৭২০/২০ দিনে
= ৩৬ দিনে ।

Question: ABCD is a square and one of its sides AB is also a chord of the circle as shown in the figure. What is the area of the square?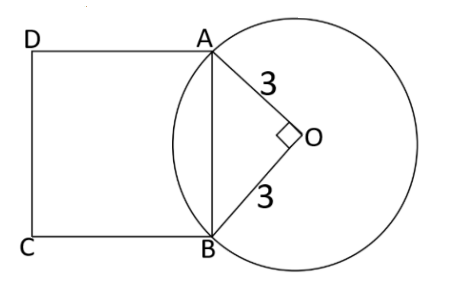


Solution:
চিত্রানুসারে, O হলো বৃত্তের কেন্দ্র এবং OA ও OB হলো বৃত্তের ব্যাসার্ধ, যার দৈর্ঘ্য 3।
 AOB একটি সমকোণী ত্রিভুজ, যেখানে ∠AOB = 90° এবং অতিভুজ = AB

পিথাগোরাসের উপপাদ্য অনুসারে,
AB2 = OA2 + OB2
AB2 = 32 + 32
AB2 = 9 + 9
AB2 = 18

আমরা জানি, বর্গক্ষেত্রের ক্ষেত্রফল = বাহুর দৈর্ঘ্য২ 
যেহেতু ABCD একটি বর্গ, তাই এর ক্ষেত্রফল হলো AB2
সুতরাং, বর্গটির ক্ষেত্রফল হলো 18

প্রশ্ন: একটি সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য লম্ব অপেক্ষা 1 মিটার কম এবং লম্ব অপেক্ষা অতিভুজের দৈর্ঘ্য 1 মিটার বেশি হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত? 

সমাধান: 
ধরি, 
সমকোণী ত্রিভুজের লম্বের দৈর্ঘ্য = x
∴ সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য = x - 1
∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = x + 1 

আমরা জানি,
(অতিভুজ)2 = (লম্ব)2 + (ভূমি)2 
⇒ (x + 1)2 = (x - 1)2 + x2 
⇒ x2 + 2x + 1 = x2 - 2x + 1 + x2 
⇒ x2 - 4x = 0 
⇒ x(x - 4) = 0 
⇒ x = 4  [যেহেতু, ত্রিভুজের লম্ব কখনো শূন্য হতে পারে না]

∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = (x + 1) মিটার 
= (4 + 1) মিটার 
= 5 মিটার ।