সমাধান: 

বেলন বা সিলিন্ডার:

- কোনো আয়তক্ষেত্রের যে কোনো বাহুকে অক্ষ ধরে আয়তক্ষেত্রটিকে ঐ বাহুর চতুর্দিকে ঘোরালে যে ঘনবস্তুর সৃষ্টি হয়, তাকে সমবৃত্তভূমিক বেলন বা সিলিন্ডার বলা হয়।

সমবৃত্তভূমিক বেলনের দুই প্রান্তকে বৃত্তাকার তল, বক্রতলকে বক্রপৃষ্ঠ এবং সমগ্রতলকে পৃষ্ঠতল বলা হয়।

- বেলনের উচ্চতা h এবং ব্যাসার্ধ r হলে -

• আয়তন (Volume) = πr2h, 

• বক্রপৃষ্ঠের ক্ষেত্রফল = 2πrh, 

• ভূমির ক্ষেত্রফল = πr2, 

• সমগ্র তলের ক্ষেত্রফল/পৃষ্ঠতলের ক্ষেত্রফল= 2πr(r + h) । 

প্রশ্ন: 5 সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র হতে 4 সে.মি. দূরবর্তী জ্যা এর দৈর্ঘ্য কত?

সমাধান:

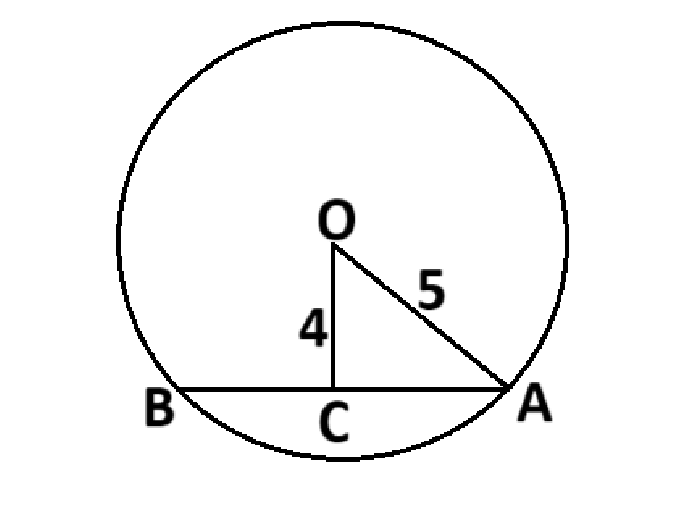
ধরি,
বৃত্তের কেন্দ্র O, 
ব্যাসার্ধ = OA = 5 সে.মি. 
O বিন্দু হতে AB জ্যা এর দূরত্ব = OC = 4 সে.মি. 

OAC সমকোণী ত্রিভুজে,
পিথাগোরাসের উপপাদ্য অনুযায়ী,
OA2 = OC2 + AC2 
⇒ AC2 = OA2 - OC2
⇒ AC2 = (5)2 - (4)2
⇒ AC2 = 25 - 16
⇒ AC2 = 9
⇒ AC = 3

C বিন্দু AB জ্যা কে সমদ্বিখণ্ডিত করে।
∴ AC = BC
∴ AB = AC + BC = AC + AC = 2AC

∴ AB = 2AC = (2 × 3) সে.মি. = 6 সে.মি. 

Question: Find the maximum distance between two points on the perimeter of a rectangular garden whose length and breadth are 24 m and 7 m.

Solution:
একটি আয়তক্ষেত্রের পরিসীমার উপর অবস্থিত দুটি বিন্দুর মধ্যে সর্বাধিক দূরত্ব হলো এর কর্ণের দৈর্ঘ্য। কর্ণের দৈর্ঘ্য পিথাগোরাসের সূত্র ব্যবহার করে নির্ণয় করা যায়।

কর্ণের দৈর্ঘ্য = √(দৈর্ঘ্য২ + প্রস্থ২)
= √(242 + 72)
= √(576 + 49)
= √625
= 25 মিটার

সুতরাং, দুটি বিন্দুর মধ্যে সর্বাধিক দূরত্ব হলো 25 মিটার।