প্রশ্ন: যদি P = 16 এবং TAP = 37 হয় তবে CUP-কত?

সমাধান:

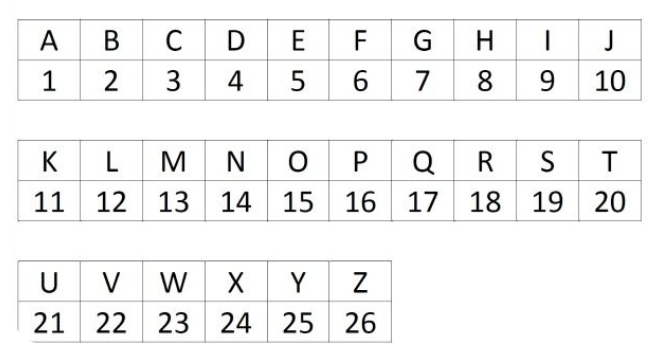
দেওয়া আছে,
P = 16
এবং TAP = 37
ইংরেজি বর্ণমালা হতে পাই,
T + A + P = 20 + 1 + 16 = 37
সেই অনুসারে,
CUP = C + U + P = 3 + 21 + 16 = 40
অর্থাৎ, CUP এর মান 40.

Question: The ratio of length and breadth of a rectangular park is 7 : 5. A man runs along its boundary at 8 km/hr and takes 9 minutes for one round. Find its area in sq. meters.

Solution:

One round of the park is equal to the perimeter of the park.

So, by completing one round, the man covers a distance equal to the perimeter of the park.

Now,

Distance or perimeter = speed × time

= 8 × (9/60)

= 1.2 km

= 1200 meters

Let,

Length = 7x and breadth = 5x

So, Perimeter,

2(7x + 5x) = 1200

⇒ 24x = 1200

∴ x =1200/24 = 50 meters

So, Length = 7 × 50 = 350 meters

And, Breadth = 5 × 50 = 250 meters

Area = Length × Breadth

= 350 × 250

= 87500 sq. m.

Question: The present ages of A and B are in the ratio 3 : 5. After 10 years, the ratio of their ages will be 4 : 6. What is the difference in their present ages?

​

​Solution:

​Let the present ages be,

​A = 3x and B = 5x

​

​Ages after 10 years,

​A = 3x + 10

​B = 5x + 10

​

​According to the problem, the ratio becomes 4 : 6

​(3x + 10) : (5x + 10) = 4 : 6

⇒ ​​(3x + 10)/(5x + 10) = 4/6

​⇒ ​​3(3x + 10) =2(5x + 10)

​⇒ ​​9x + 30 = 10x + 20

⇒ ​​​10x - 9x = 30 - 20

∴ ​x = 10

​

​A = 3 × 10 = 30 years

​B = 5 × 10 = 50 years

​

∴ Difference = 50 - 30 = 20 years