a + b + c = 6 এবং a2+ b2 + c2 = 14 হলে ab + bc + ca এর মান কত?
A
11
B
14
C
20
D
29
উত্তরের বিবরণ
প্রশ্ন: a + b + c = 6 এবং a2+ b2 + c2 = 14 হলে ab + bc + ca এর মান কত?
সমাধান:
দেওয়া আছে,
a + b + c = 6 এবং a2 + b2 + c2 =14
আমরা জানি,
(a + b + c)2 = ( a2 + b2 + c2) + 2(ab + bc + ca)
⇒ (6)2 =14 + 2(ab + bc + ca)
⇒ 36 = 14 + 2(ab + bc + ca)
⇒ 36 - 14 = 2(ab + bc + ca)
⇒ 22 = 2(ab + bc + ca)
⇒ ab + bc + ca = 22/2
⇒ ab + bc + ca = 11
0
Updated: 1 month ago
x = (1/x) + (3/2) হলে, 8{x3 - (1/x3)} = কত?
Created: 3 weeks ago
A
63
B
62
C
61
D
60
প্রশ্ন: x = (1/x) + (3/2) হলে, 8{x3 - (1/x3)} = কত?
সমাধান:
x = (1/x) + (3/2)
⇒ x - (1/x) = 3/2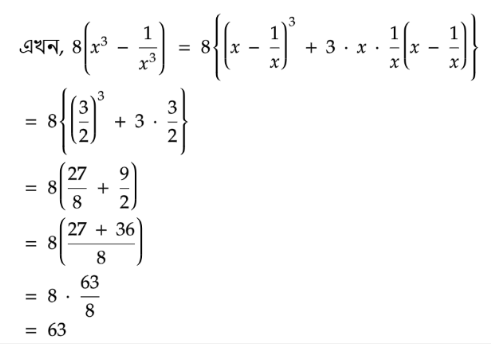
0
Updated: 3 weeks ago
How many terms are there in the geometric progression,
3, 6, 12, 24, …, 1536
Created: 1 week ago
A
10
B
8
C
11
D
9
Question: How many terms are there in the geometric progression,
3, 6, 12, 24, …, 1536
Solution:
First term, a = 3
Common ratio, r = 6/3 = 2
Last term or nth term of GP = arn - 1
⇒ 1536 = 3 × (2n - 1)
⇒ 2n - 1 = 1536/3
⇒ 2n - 1 = 512
⇒ 2n - 1 = 29
So, comparing the power,
Thus, n - 1 = 9
∴ n = 10
∴ Number of terms = 10
0
Updated: 1 week ago
2 + 4 + 6 + 8 +.................. ধারাটির প্রথম n সংখ্যক পদের সমষ্টি 2550 হলে, n এর মান কত?
Created: 1 month ago
A
49
B
50
C
51
D
53
প্রশ্ন: 2 + 4 + 6 + 8 +.................. ধারাটির প্রথম n সংখ্যক পদের সমষ্টি 2550 হলে, n এর মান কত?
সমাধান:
দেওয়া আছে,
ধারাটির প্রথম পদ, a = 2
সাধারণ অন্তর, d = 4 - 2 = 2
সমান্তর ধারার n-তম পদের সমষ্টি = (n/2){2a + (n - 1)d}
প্রশ্নমতে,
(n/2){2a + (n - 1)d} = 2550
⇒ (n/2){(2 × 2) + (n - 1)2} = 2550
⇒ (n/2)(4 + 2n - 2) = 2550
⇒ (n/2)(2n + 2) = 2550
⇒ (n/2) × 2(n + 1) = 2550
⇒ n(n + 1) - 2550 = 0
⇒ n2 + n - 2550 = 0
⇒ n2 + 51n - 50n - 2550 = 0
⇒ n(n + 51) - 50(n + 51) = 0
⇒ (n + 51)(n - 50) = 0
হয়, n + 51 = 0 অথবা n - 50 = 0
হয়, n = - 51 অথবা n = 50
যেহেতু পদসংখ্যা ঋণাত্মক হতে পারে না। তাই n = - 51 গ্রহণযোগ্য নয়।
∴ পদসংখ্যা, n = 50
0
Updated: 1 month ago