তিন সদস্যের একটি বিতর্ক দলের সদস্যদের গড় বয়স ২৪ বছর। যদি কোনো সদস্যের বয়সই ২১ বছরের নিচে না হয় তবে তাদের কোনো একজনের সর্বোচ্চ বয়স কত হতে পারে?
A
২৫ বছর
B
৩০ বছর
C
২৮ বছর
D
৩২ বছর
উত্তরের বিবরণ
প্রশ্ন: তিন সদস্যের একটি বিতর্ক দলের সদস্যদের গড় বয়স ২৪ বছর। যদি কোনো সদস্যের বয়সই ২১ বছরের নিচে না হয়, তবে তাদের কোনো একজনের সর্বোচ্চ বয়স কত?
সমাধান:
তিন সদস্যের গড় বয়স = ২৪ বছর
∴ তিন সদস্যের গড় বয়সের সমষ্টি = (২৪ × ৩) বছর
= ৭২ বছর
আবার,
দুই সদস্যের গড় বয়স = ২১ বছর
∴ দুই সদস্যের গড় বয়সের সমষ্টি = (২১ × ২) বছর
= ৪২ বছর
∴ একজনের সর্বোচ্চ বয়স = (৭২ - ৪২) বছর
= ৩০ বছর
0
Updated: 1 month ago
4 জন মহিলা ও 6 জন পুরুষের মধ্য থেকে 4 সদস্যবিশিষ্ট একটি উপ-কমিটি গঠন করতে হবে যাতে 1 জন নির্দিষ্ট পুরুষ সর্বদাই উপস্থিত থাকেন। কত প্রকারে ঐ কমিটি গঠন করা যেতে পারে?
Created: 1 month ago
A
210
B
304
C
84
D
120
প্রশ্ন: 4 জন মহিলা ও 6 জন পুরুষের মধ্য থেকে 4 সদস্যবিশিষ্ট একটি উপ-কমিটি গঠন করতে হবে যাতে 1 জন নির্দিষ্ট পুরুষ সর্বদাই উপস্থিত থাকেন। কত প্রকারে ঐ কমিটি গঠন করা যেতে পারে?
সমাধান:
যেহেতু 1 জন পুরুষ সর্বদাই উপস্থিত থাকবে তাই
4 + (6 - 1) = 4 + 5 = 9 জন থেকে বাকি 3 সদস্য বাছাই করা যাবে = 9C3 = 84
0
Updated: 1 month ago
একটি আয়তক্ষেত্রের দৈর্ঘ্য প্রস্থের ৩ গুণ। আয়তক্ষেত্রটির ক্ষেত্রফল ৩০০ বর্গমিটার হলে তার পরিসীমা কত?
Created: 2 months ago
A
৭০ মিটার
B
৭৫ মিটার
C
৮০ মিটার
D
৯০ মিটার
প্রশ্ন: একটি আয়তক্ষেত্রের দৈর্ঘ্য প্রস্থের ৩ গুণ। আয়তক্ষেত্রটির ক্ষেত্রফল ৩০০ বর্গমিটার হলে তার পরিসীমা কত?
সমাধান:
ধরি,
আয়তক্ষেত্রের প্রস্থ x মিটার
∴ আয়তক্ষেত্রের দৈর্ঘ্য 3x মিটার
আয়তক্ষেত্রের ক্ষেত্রফল = 3x2 বর্গমিটার
প্রশ্নমতে,
3x2 = 300
⇒ x2 = 100
⇒ x = 10
আয়তক্ষেত্রের প্রস্থ 10 মিটার
∴ আয়তক্ষেত্রের দৈর্ঘ্য 3 × 10 মিটার = 30 মিটার
আয়তক্ষেত্রের পরিসীমা 2(30 + 10) মিটার
= 2 × 40 মিটার
= 80 মিটার
0
Updated: 2 months ago
একটি মিনারের পাদদেশ হতে ২০ মিটার দূরের একটি স্থান হতে মিনারটির শীর্ষবিন্দুর উন্নতি কোণ 30° হলে মিনারটির উচ্চতা কত?
Created: 2 months ago
A
20√7 মিটার
B
20/√3 মিটার
C
20 মিটার
D
10√3 মিটার
প্রশ্ন: একটি মিনারের পাদদেশ হতে ২০ মিটার দূরের একটি স্থান হতে মিনারটির শীর্ষবিন্দুর উন্নতি কোণ 30° হলে মিনারটির উচ্চতা কত?
সমাধান:
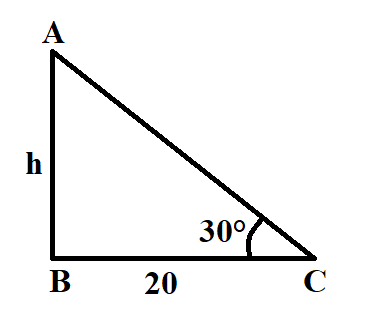
ধরি,
মিনারটির উচ্চতা, AB = h
মিনারের পাদদেশ হতে BC = ২০ মিটার দূরের একটি স্থান হতে মিনারটির শীর্ষ বিন্দুর উন্নতি কোণ ∠ACB = ৩০°
আমরা জানি,
tan∠ACB = AB/BC
বা, tan30° = h/20
বা, 1/√3 = h/20
∴ h = 20/√3
∴ মিনারটির উচ্চতা = 20/√3
0
Updated: 2 months ago