2, 8 এবং
32 এর জ্যামিতিক গড় কত?
A
9.33
B
9
C
8
D
7
উত্তরের বিবরণ
সমাধানঃ
আমরা জানি,
n সংখ্যক সংখ্যার গুণোত্তর গড় বা জ্যামিতিক গড় 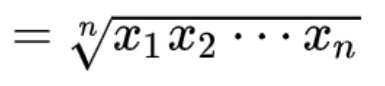
∴ 2, 8 এবং 32 এর জ্যামিতিক গড় = (2 × 8 × 32)1/3
= (512)1/3
= (83)1/3
= 8
0
Updated: 2 months ago
3cm, 4cm এবং 5cm ব্যাসার্ধ বিশিষ্ট তিনটি গোলক গলিয়ে একটি গোলক তৈরি করা হলে গোলকের ব্যাসার্ধ কত?
Created: 1 month ago
A
12 সে.মি.
B
6 সে.মি.
C
4 সে.মি.
D
8 সে.মি.
শ্ন: 3cm, 4cm এবং 5cm ব্যাসার্ধ বিশিষ্ট তিনটি গোলক গলিয়ে একটি গোলক তৈরি করা হলে গোলকের ব্যাসার্ধ কত?
সমাধান:
আমরা জানি,
গোলকের আয়তন = (4/3)πr3
3 সে.মি., 4 সে.মি. ও 5 সে.মি. ব্যাসার্ধ বিশিষ্ট গোলক তিনটির আয়তন যথাক্রমে,
{(4/3)π × 33}, {(4/3)π × 43} {(4/3)π × 53}
সুতরাং নতুন গোলকটির আয়তন ={(4/3)π × 33} + {(4/3)π × 43} + {(4/3)π × 53}
= (4/3)π × (33 + 43 + 53)
= (4/3)π × (27 + 64 + 125)
= (4/3)π × 216
= (4/3)π × 63
∴ নতুন গোলকটির ব্যাসার্ধ = 6 সে.মি.
0
Updated: 1 month ago
PQR ত্রিভুজের PN একটি মধ্যমা এবং M ভরকেন্দ্র। যদি মধ্যমা PN-এর দৈর্ঘ্য ২১ সেমি হয়, তাহলে PM-এর দৈর্ঘ্য কত?
Created: 1 month ago
A
১৪ সেমি
B
২১ সেমি
C
৩৬ সেমি
D
১৮ সেমি
প্রশ্ন: PQR ত্রিভুজের PN একটি মধ্যমা এবং M ভরকেন্দ্র। যদি মধ্যমা PN-এর দৈর্ঘ্য ২১ সেমি হয়, তাহলে PM-এর দৈর্ঘ্য কত?
সমাধান:
আমরা জানি,
কোনো ত্রিভুজের ভরকেন্দ্র তার মধ্যমাকে ২ : ১ অনুপাতে বিভক্ত করে।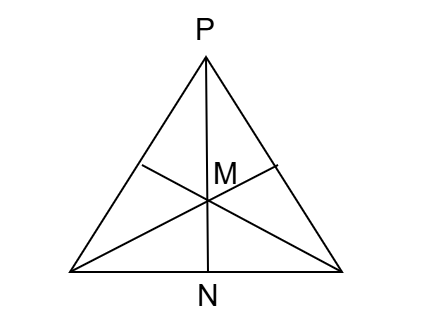
এখানে,
PN মধ্যমা এবং M ভরকেন্দ্র।
∴ PM : MN = ২ : ১
মোট অনুপাত = ২ + ১ = ৩
মধ্যমা PN-এর দৈর্ঘ্য = ২১ সেমি
ভরকেন্দ্র M, মধ্যমা PN-কে দুটি অংশে বিভক্ত করেছে: PM এবং MN।
∴ PM-এর দৈর্ঘ্য = ২১ এর (২/৩) অংশ
= ২১ × (২/৩) সেমি
= ১৪ সেমি
সুতরাং, PM-এর দৈর্ঘ্য ১৪ সেমি।
0
Updated: 1 month ago
একটি ত্রিভুজ ও একটি বৃত্ত ন্যূনতম কয়টি বিন্দুতে ছেদ করে?
Created: 4 weeks ago
A
দুইটি
B
একটি
C
তিনটি
D
চারটি
প্রশ্ন: একটি ত্রিভুজ ও একটি বৃত্ত ন্যূনতম কয়টি বিন্দুতে ছেদ করে?
সমাধান:
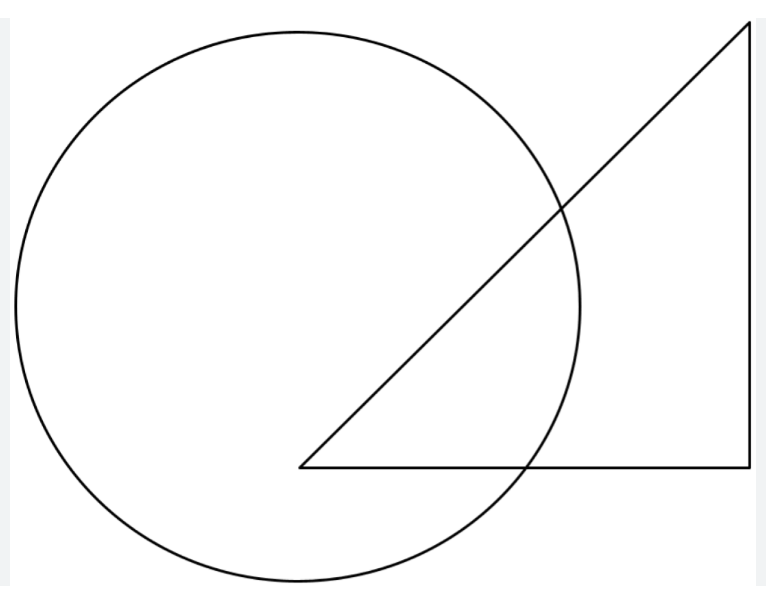
- একটি ত্রিভুজ ও একটি বৃত্ত ন্যূনতম দুইটি বিন্দুতে ছেদ করতে পারে।
কারণ, ত্রিভুজের বাহু অবশ্যই বৃত্তের দুটি বিন্দুতে ছেদ করলে উহা ছেদক হবে।
0
Updated: 4 weeks ago