যদি ঙ × N = 70 হয়, তবে ট × J = ?
A
108
B
152
C
110
D
120
উত্তরের বিবরণ
প্রশ্ন: যদি ঙ × N = 70 হয়, তবে ট × J = ?
সমাধান:
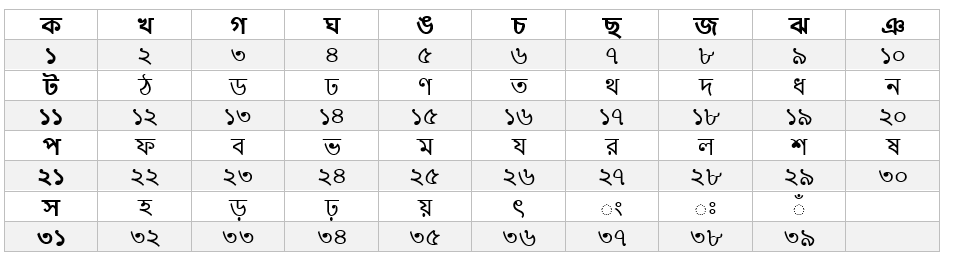
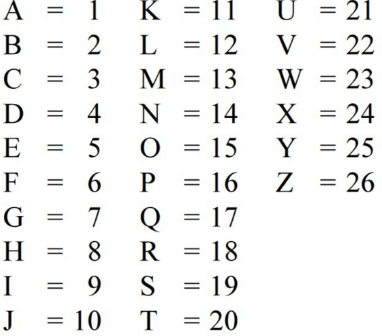
ঙ × N = 5 × 14 = 70
এবং ট × J = 11 × 10 = 110
0
Updated: 2 months ago
সর্বনিম্ন কত সংখ্যক ছাত্রকে ৬, ৯ এবং ১৫ জনের দলে ভাগ করে এবং তাদেরকে বর্গাকৃতিতে সাজানো সম্ভব?
Created: 1 month ago
A
৯০০ জন
B
৩৬০০ জন
C
১২০০ জন
D
১৬০০ জন
প্রশ্ন: সর্বনিম্ন কত সংখ্যক ছাত্রকে ৬, ৯ এবং ১৫ জনের দলে ভাগ করে এবং তাদেরকে বর্গাকৃতিতে সাজানো সম্ভব?
সমাধান:
৬, ৯ এবং ১৫ এর ল.সা.গু. নির্ণয় করি,
৬ = ২ × ৩
৯ = ৩ × ৩
১৫ = ৩ × ৫
∴ ল.সা.গু. = ২ × ৩ × ৩ × ৫
এখন,ছাত্রদেরকে বর্গাকৃতিতে সাজানো সম্ভব হলে মোট ছাত্রসংখ্যা অবশ্যই একটি পূর্ণবর্গ সংখ্যা হবে। কোনো সংখ্যা পূর্ণবর্গ হতে হলে তার মৌলিক উৎপাদকগুলোর সূচক (power) অবশ্যই জোড় সংখ্যা হতে হবে।
∴ লসাগু এর সাথে ২ এবং ৫ দ্বারা গুণ করতে হবে।
∴ ছাত্রসংখ্যা = (২ × ২) × (৩ × ৩) × (৫ × ৫) = ৯০০
0
Updated: 1 month ago
1/√3, - 1, √3, ......... ধারটির পঞ্চম পদ কত?
Created: 1 month ago
A
3√3
B
- 9√3
C
9
D
√3
সমাধান ব্যাখ্যা:
প্রদত্ত জ্যামিতিক ধারা:
১. প্রথম পদ:
২. সাধারণ অনুপাত (r):
৩. জ্যামিতিক ধারার n-তম পদ সূত্র:
৪. পঞ্চম পদ (n = 5):
উত্তর: পঞ্চম পদ = 3√3
0
Updated: 1 month ago
5 × 3 = 4527 এবং 9 × 4 = 8136 হলে 8 × 2 = ?
Created: 3 weeks ago
A
7218
B
2436
C
6336
D
5614
প্রশ্ন: 5 × 3 = 4527 এবং 9 × 4 = 8136 হলে 8 × 2 = ?
সমাধান:
5 × 3 = 4527 এবং 9 × 4 = 8136 হলে 8 × 2 = 7218
5 × 9 = 45 [9 দ্বারা গুণ করে]
3 × 9 = 27 [9 দ্বারা গুণ করে]
∴ 5 × 3 = 4527 [গুণফলদ্বয়কে পাশাপাশি বসিয়ে]
এবং
9 × 9 = 63 [9 দ্বারা গুণ করে]
4 × 9 = 36 [9 দ্বারা গুণ করে]
∴ 9 × 4 = 8136 [গুণফলদ্বয়কে পাশাপাশি বসিয়ে]
অনুরূপভাবে,
8 × 9 = 72 [9 দ্বারা গুণ করে]
2 × 9 = 18 [9 দ্বারা গুণ করে]
∴ 8 × 2 = 7218 [গুণফলদ্বয়কে পাশাপাশি বসিয়ে]
0
Updated: 3 weeks ago