প্রশ্নবোধক স্থানে কোন সংখ্যা বসবে?
A
২৯
B
৪৫
C
৩১
D
৫৯
উত্তরের বিবরণ
প্রশ্ন: প্রশ্নবোধক স্থানে কোন সংখ্যা বসবে?
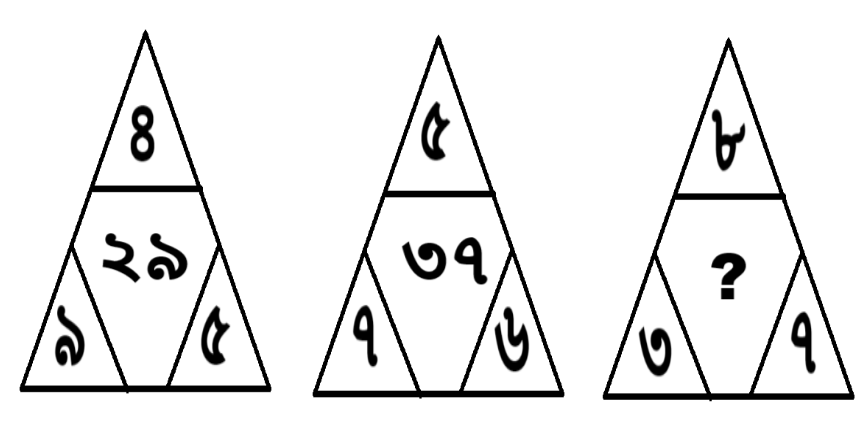
সমাধান:
এখানে,
(নিচের ডান পাশের ত্রিভুজ × উপরের ত্রিভুজ) + নিচের বাম পাশের ত্রিভুজ = মাঝখানের সংখ্যা
১ম ত্রিভুজ,
(৫ × ৪) + ৯ = ২০ + ৯ = ২৯
২য় ত্রিভুজ,
(৬ × ৫) + ৭ = ৩০ + ৭ = ৩৭
৩য় ত্রিভুজ,
(৭ × ৮) + ৩ = ৫৬ + ৩ = ৫৯
∴ প্রশ্নবোধক স্থানে ৫৯ সংখ্যাটি বসবে।
0
Updated: 2 months ago
যদি ২০২৫ সালের নভেম্বর মাসের ১ তারিখ শনিবার হয়, তাহলে ডিসেম্বর মাসের ১৮ তারিখ কী বার হবে?
Created: 3 weeks ago
A
শুক্রবার
B
বৃহস্পতিবার
C
মঙ্গলবার
D
বুধবার
প্রশ্ন: যদি ২০২৫ সালের নভেম্বর মাসের ১ তারিখ শনিবার হয়, তাহলে ডিসেম্বর মাসের ১৮ তারিখ কী বার হবে?
সমাধান:
৭ দিন পর ৮ম দিনে পুনরায় একই বার আসে।
তাই নভেম্বর মাসের ১ম দিন শনিবার হলে ৮ম, ১৫তম, ২২তম, ২৯তম দিন শনিবার হবে এবং ডিসেম্বর মাসের ৬তম ও ১৩ তম দিন শনিবার হবে।
এখন,
ডিসেম্বর মাসের ১৩ তারিখ হবে শনিবার।
ডিসেম্বর মাসের ১৪ তারিখ হবে রবিবার।
ডিসেম্বর মাসের ১৫ তারিখ হবে সোমবার।
ডিসেম্বর মাসের ১৬ তারিখ হবে মঙ্গলবার ।
ডিসেম্বর মাসের ১৭ তারিখ হবে বুধবার।
ডিসেম্বর মাসের ১৮ তারিখ হবে বৃহস্পতিবার।
0
Updated: 3 weeks ago
একটি চাকার ব্যাস ৪.২ মিটার। ২৬৪ মিটার পথ অতিক্রম করতে চাকাটি কতবার ঘুরবে?
Created: 1 month ago
A
১০ বার
B
১৫ বার
C
২০ বার
D
২৫ বার
প্রশ্ন: একটি চাকার ব্যাস ৪.২ মিটার। ২৬৪ মিটার পথ অতিক্রম করতে চাকাটি কতবার ঘুরবে?
সমাধান:দেওয়া আছে,
চাকার ব্যাস, ২r = ৪.২ মিটার
ব্যাসার্ধ, r = ৪.২/২ = ২.১ মিটার
চাকার পরিধি = ২πr = ২ × (২২/৭) × ২.১ = ১৩.২ মিটার
আমরা জানি,
চাকাটি একবার ঘুরলে পরিধির সমান দূরত্ব অতিক্রম করে।
এখন,
১৩.২ মিটার দূরত্ব অতিক্রম করলে চাকাটি ঘুরবে = ১ বার
∴ ২৬৪ মিটার দূরত্ব অতিক্রম করলে চাকাটি ঘুরবে = ২৬৪/১৩.২ = ২০ বার
চাকার ব্যাস, ২r = ৪.২ মিটার
ব্যাসার্ধ, r = ৪.২/২ = ২.১ মিটার
চাকার পরিধি = ২πr = ২ × (২২/৭) × ২.১ = ১৩.২ মিটার
আমরা জানি,
চাকাটি একবার ঘুরলে পরিধির সমান দূরত্ব অতিক্রম করে।
এখন,
১৩.২ মিটার দূরত্ব অতিক্রম করলে চাকাটি ঘুরবে = ১ বার
∴ ২৬৪ মিটার দূরত্ব অতিক্রম করলে চাকাটি ঘুরবে = ২৬৪/১৩.২ = ২০ বার
0
Updated: 1 month ago
1/√3, - 1, √3, ......... ধারটির পঞ্চম পদ কত?
Created: 1 month ago
A
3√3
B
- 9√3
C
9
D
√3
সমাধান ব্যাখ্যা:
প্রদত্ত জ্যামিতিক ধারা:
১. প্রথম পদ:
২. সাধারণ অনুপাত (r):
৩. জ্যামিতিক ধারার n-তম পদ সূত্র:
৪. পঞ্চম পদ (n = 5):
উত্তর: পঞ্চম পদ = 3√3
0
Updated: 1 month ago