O কেন্দ্র বিশিষ্ট বৃত্তের অন্তর্লিখিত ABC ত্রিভুজে ∠BOC =118° হলে ∠BCO = ?
A
27°
B
31°
C
36°
D
62°
উত্তরের বিবরণ
সমাধান:

OC ও OB বৃত্তের ব্যাসার্ধ বলে OC = OB
ΔBOC একটি সমদ্বিবাহু ত্রিভুজ।
এখন,
ΔBOC সমদ্বিবাহু ত্রিভুজে, ∠OBC = ∠BCO
আবার,
ΔBOC এ,
∠OBC + ∠BOC + ∠BCO = 180°
⇒ ∠BCO + ∠BOC + ∠BCO = 180 [∠OBC = ∠BCO]
⇒ 2 BCO + BOC = 180°
⇒ 2 ∠BCO + 118° = 180°
⇒ 2 ∠BCO = 180° - 118° = 62°
⇒ ∠BCO = 62°/2
⇒ ∠BCO = 31°
0
Updated: 2 months ago
2 সে. মি. ব্যাসার্ধবিশিষ্ট একটি বৃত্তের অন্তঃস্থ একটি বর্গক্ষেত্রের চারটি বাহু এবং বৃত্তটি দ্বারা আবদ্ধ অঞ্চলের ক্ষেত্রফল কত বর্গ সে.মি.?
Created: 1 month ago
A
4π - 8
B
4π + 8
C
2π - 4
D
2π + 4
প্রশ্ন: 2 সে.মি. ব্যাসার্ধ বিশিষ্ট একটি বৃত্তের অন্তঃস্থ একটি বর্গক্ষেত্রের বহিঃস্থ এবং বৃত্তটি দ্বারা আবৃদ্ধ অঞ্চলের ক্ষেত্রফল কত বর্গ সেন্টিমিটার?
সমাধান:
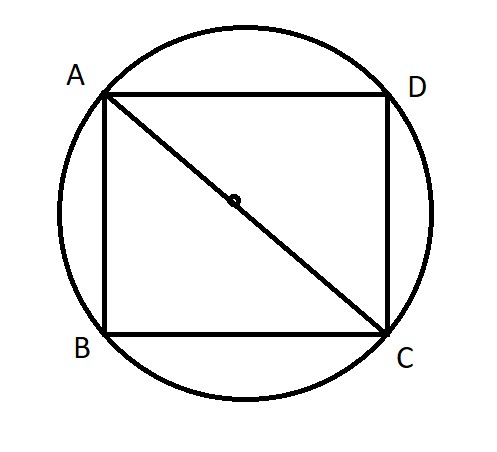
মনেকরি
বৃত্তের ব্যাসার্ধ r = 2 সে.মি
বৃত্তের ক্ষেত্রফল = πr2 = π × 22 বর্গ সে.মি
=4π বর্গ সে.মি
আবার
ABCD এ AC = 4 সে.মি.
আমরা জানি
AC2 = AB2 + BC2
⇒ AB2 + AB2 = AC2
⇒ 2AB2 = 42
⇒ 2AB2 =16
∴ AB2 = 8
বর্গক্ষেত্রের বহিঃস্থ এবং বৃত্তটি দ্বারা আবৃদ্ধ অঞ্চলের ক্ষেত্রফল = 4π - 8 বর্গ সে.মি
0
Updated: 1 month ago
ABCD সামান্তরিকে ∠B = 80° হলে, ∠A + ∠C = ?
Created: 1 week ago
A
200°
B
220°
C
250°
D
260°
প্রশ্ন: ABCD সামান্তরিকে ∠B = 80° হলে, ∠A + ∠C = ?
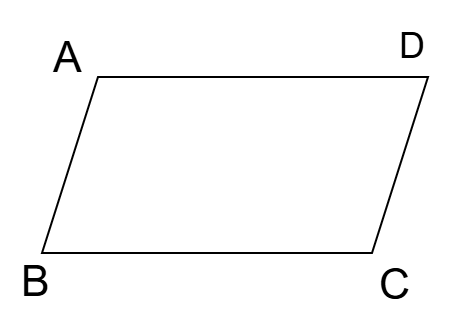
সমাধান:
আমরা জানি, একটি সামান্তরিকের বিপরীত কোণগুলো পরস্পর সমান এবং এর যেকোনো দুটি সন্নিহিত কোণের সমষ্টি 180°।
এখানে, ∠B = 80°।
যেহেতু ∠A এবং ∠B সন্নিহিত কোণ,
অতএব, ∠A + ∠B = 180°
বা, ∠A + 80° = 180°
বা, ∠A = 180° - 80°
∴ ∠A = 100°
আবার, সামান্তরিকের বিপরীত কোণগুলো সমান হওয়ায়,
∠A = ∠C = 100°
সুতরাং, ∠A + ∠C = 100° + 100° = 200°
0
Updated: 1 week ago
একটি বিন্দু দিয়ে কতটি সরলরেখা টানা যায়?
Created: 4 weeks ago
A
একটি
B
দুইটি
C
অসংখ্য
D
কোনোটিই নয়
প্রশ্ন: একটি বিন্দু দিয়ে কতটি সরলরেখা টানা যায়?
সমাধান:
বিন্দু (Point):
- বিন্দুর কেবল অবস্থান আছে, কিন্তু দৈর্ঘ্য, প্রস্থ ও বেদ নাই।
- বিন্দুর শুধু অবস্থান আছে কিন্তু কোন মাত্রা নেই এবং বিন্দু মাত্রাহীন।
- পেনসিলের সরু মাথা দিয়ে কাগজে ফোঁটা দিলে একে বিন্দুর প্রতিকৃতি বলে ধরা হয়।
বিন্দুর শ্রেণিবিভাগ:
- বিন্দুকে সাধারণত ৩ শ্রেণিতে ভাগ করা হয়েছে।
যথা- i. সমরেখ বিন্দু, ii. অসমরেখ বিন্দু ও iii. সমবিন্দু।
সাধারণ বিন্দু:
- একটি সমতলে দুটি সরলরেখা যে নির্দিষ্ট বিন্দুটিতে ছেদ করে সেই বিন্দুটিকেই সাধারণ বিন্দু বলে।
- দুটি বিন্দু দিয়ে একটি সরলরেখা টানা যায়, কিন্ত একাধিক বক্ররেখা টানা যায় না।
- একটি বিন্দু দিয়ে একাধিক বিন্দু সংযোগকারী সরলরেখা টানা যায়।
- সরলরেখা পরস্পরকে ছেদ করতে পারে।
0
Updated: 4 weeks ago