xy-কে দুটি বর্গের অন্তরফল রূপে প্রকাশ করলে পাওয়া যাবে-
A
xy=(x+y)2/2−(x−y)2/2
B
xy=(x−y)2/2−(x+y)2/2
C
xy=(x+y)2−(x−y)2
D
xy = ((x+y)/2)2 - ((x-y)/2)2
উত্তরের বিবরণ
সমাধান :
আমরা জানি, দুটি বর্গের অন্তর (Difference of Squares) হলো—
এখন আমরা –কে এমনভাবে সাজাতে চাই যাতে এটি দুটি বর্গের অন্তররূপে প্রকাশ করা যায়।
ধরি,
এখন হিসাব করলে পাই—
এখন Difference of Squares সূত্র প্রয়োগ করি—
এখানে,
সুতরাং,
অর্থাৎ, আমরা সফলভাবে দেখাতে পারলাম যে—
উত্তরঃ
0
Updated: 9 hours ago
একটি সমকোণী ত্রিভুজের অতিভুজ 25 মিটার। অপর বাহুদ্বয়ের একটি অপরটির 3/4 অংশ হলে, অপর বাহুদ্বয়ের দৈর্ঘ্য অনুপাত-
Created: 2 weeks ago
A
3 : 4
B
1 : 2
C
3 : 5
D
2 : 1
প্রশ্নঃ একটি সমকোণী ত্রিভুজের অতিভুজ ২৫ মিটার। অপর বাহুদ্বয়ের একটি অপরটির ৩/৪ অংশ হলে, অপর বাহুদ্বয়ের দৈর্ঘ্য অনুপাত নির্ণয় কর।
সমাধানঃ
ধরা যাক, অপর দুই বাহু যথাক্রমে ( x ) মিটার এবং ( \frac{3x}{4} ) মিটার।
অতিভুজ = ২৫ মিটার।
পাইথাগোরাসের সূত্র অনুযায়ী,
অতিভুজ² = প্রথম বাহু² + দ্বিতীয় বাহু²
অতএব,
( 25² = x² + \left(\frac{3x}{4}\right)² )
⇒ ( 625 = x² + \frac{9x²}{16} )
⇒ ( 625 = \frac{16x² + 9x²}{16} )
⇒ ( 625 = \frac{25x²}{16} )
⇒ ( x² = \frac{625×16}{25} )
⇒ ( x² = 400 )
⇒ ( x = 20 )
অতএব, অপর দুটি বাহু হলো ২০ মিটার এবং ( \frac{3×20}{4} = ১৫ ) মিটার।
সুতরাং, অপর বাহুদ্বয়ের দৈর্ঘ্য অনুপাত = ১৫ : ২০ = ৩ : ৪
উত্তরঃ ক) ৩ : ৪
0
Updated: 2 weeks ago
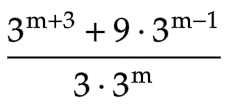এর মান কত?
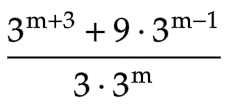এর মান কত?Created: 1 month ago
A
24
B
10
C
8/3
D
15
শ্ন: 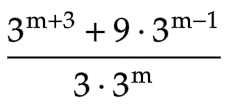এর মান কত?
সমাধান: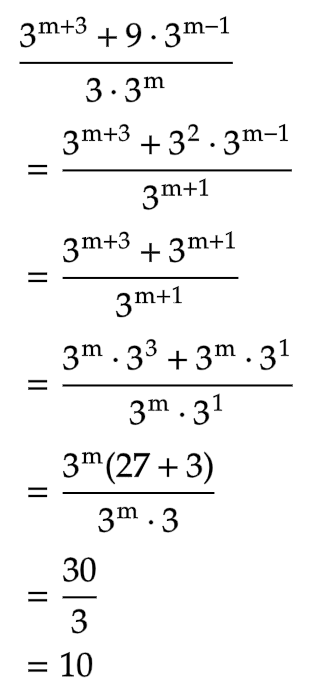
0
Updated: 1 month ago
২/৫, ৩/৫, ৬/১৫ এর গ.সা.গু কোনটি?
Created: 3 weeks ago
A
৬/৫
B
৭/৫
C
৮/৫
D
১/১৫
প্রশ্নঃ ২/৫, ৩/৫, ৬/১৫ এর গ.সা.গু নির্ণয় করো।
সমাধানঃ
প্রথমে লবগুলোর গ.সা.গু নির্ণয় করা যাক —
২, ৩ ও ৬ এর গ.সা.গু = ১
এরপর হরগুলোর ল.সা.গু নির্ণয় করা যাক —
৫, ৫ ও ১৫ এর ল.সা.গু = ১৫
অতএব, ভগ্নাংশগুলোর গ.সা.গু = লবের গ.সা.গু / হরের ল.সা.গু
= ১ / ১৫
উত্তরঃ ১/১৫
0
Updated: 3 weeks ago
