বৃত্তের বৃহত্তম জ্যা কে কি বলে?
A
ব্যাসার্ধ
B
পরিধি
C
ব্যাস
D
চাপ
উত্তরের বিবরণ
একটি বৃত্তে বিভিন্ন ধরনের সরলরেখা অংশ থাকে, কিন্তু সবার মধ্যে একটি রেখাই সর্বোচ্চ দৈর্ঘ্যের হয় এবং সেটিই বৃত্তের গঠন বোঝার জন্য সবচেয়ে গুরুত্বপূর্ণ। নিচে এ সম্পর্কে প্রয়োজনীয় তথ্যগুলো তালিকা আকারে তুলে ধরা হলো।
-
জ্যা হলো বৃত্তের পরিধির দুটি বিন্দুকে সংযুক্তকারী সরলরেখা। জ্যার দৈর্ঘ্য ছোট বা বড় হতে পারে।
-
বৃত্তের সর্বাধিক দীর্ঘ জ্যা হলো ব্যাস, কারণ এটি কেন্দ্রের মধ্য দিয়ে যায় এবং বৃত্তকে দুই সমান অংশে ভাগ করে।
-
ব্যাস সবসময় দুটি ব্যাসার্ধের সমষ্টির সমান, অর্থাৎ ব্যাস = 2 × ব্যাসার্ধ।
-
বৃত্তের যে কোন বিন্দু থেকে কেন্দ্র পর্যন্ত দূরত্বকে ব্যাসার্ধ (Radius) বলে। সকল ব্যাসার্ধ একই দৈর্ঘ্যের হয়।
-
বৃত্তকে ঘিরে থাকা পুরো বেষ্টনিকে পরিধি বলা হয়, যা বৃত্তের আকারের সাথে সরাসরি সম্পর্কযুক্ত।
-
পরিধির কোনও অংশবিশেষকে চাপ বা বৃত্তচাপ (Arc) বলা হয়, যার দুই প্রান্ত কেন্দ্রের সাথে যুক্ত হলে একটি কেন্দ্রীয় কোণ সৃষ্টি করে।
-
বৃত্ত সম্পর্কিত সব উপাদানের মধ্যে ব্যাসই একমাত্র সরলরেখা যা সর্বোচ্চ দৈর্ঘ্যের এবং বৃত্তের জ্যাগুলোর মধ্যে “বৃহত্তম জ্যা” হিসেবে বিবেচিত হয়।
0
Updated: 15 hours ago
ABC ত্রিভুজে AB = 8 মিটার, BC = 10 মিটার এবং ক্ষেত্রফল 20√3 বর্গমিটার হলে, ∠B = ?
Created: 2 months ago
A
30°
B
60°
C
90°
D
45°
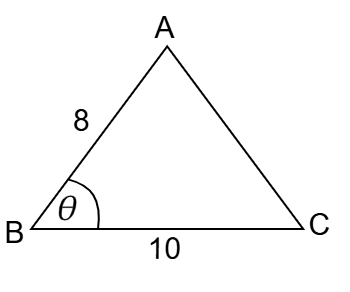
প্রশ্ন: ABC ত্রিভুজে AB = 8 মিটার, BC = 10 মিটার এবং ক্ষেত্রফল 20√3 বর্গমিটার হলে, ∠B = ?
সমাধান:
দেওয়া আছে,
AB = 8 মিটার
BC = 10 মিটার
এবং ABC ত্রিভুজে ক্ষেত্রফল = 20√3 বর্গমিটার
আমরা জানি,
একটি ত্রিভুজের সন্নিহিত বাহুদ্বয় a, b হলে এবং তাদের অন্তর্ভুক্ত কোণ θ হলে,
ক্ষেত্রফল = (1/2)ab sinθ
∴ ত্রিভুজ ABC এর ক্ষেত্রফল = (1/2) × AB × BC × sinθ
⇒ 20√3 = (1/2) × 8 × 10 × sin ∠B
⇒ 20√3 = 40 × sin ∠B
⇒ sin ∠B = 20√3/40
⇒ sin ∠B = √3/2
⇒ sin ∠B = sin 60°
⇒ ∠B = 60°
0
Updated: 2 months ago
ΔABC এ ∠A = 40°, ∠B = 70°, হলে ΔABC কী ধরনের ত্রিভুজ?
Created: 2 months ago
A
সমকোণী
B
স্থূলকোণী
C
সমদ্বিবাহু
D
সমবাহু
প্রশ্ন: ΔABC এ ∠A = 40°, ∠B = 70°, হলে ΔABC কী ধরনের ত্রিভুজ?
সমাধান:
দেওয়া আছে,
ΔABC এর ∠A = 40°, ∠B = 70°
∴ অপর কোণটি = 180° - (40° + 70°)
= 180° - 110°
= 70°
এখানে, সমান সমান কোণের বিপরীত বাহুগুলো সমান।
তাই, ΔABC একটি সমদ্বিবাহু ত্রিভুজ।
0
Updated: 2 months ago
একটি বর্গক্ষেত্র ও একটি রম্বসের ক্ষেত্রফল সমান। রম্বসের কর্ণদ্বয় যথাক্রমে ১৮ মিটার ও ৯ মিটার হলে, বর্গক্ষেত্রটির পরিসীমা কত?
Created: 2 months ago
A
৩০ মিটার
B
৩৬ মিটার
C
৪০ মিটার
D
৪৮ মিটার
প্রশ্ন: একটি বর্গক্ষেত্র ও একটি রম্বসের ক্ষেত্রফল সমান। রম্বসের কর্ণদ্বয় যথাক্রমে ১৮ মিটার ও ৯ মিটার হলে, বর্গক্ষেত্রটির পরিসীমা কত?
সমাধান:
দেওয়া আছে,
রম্বসের কর্ণদ্বয় যথাক্রমে ১৮ মিটার ও ৯ মিটার
∴ রম্বসের ক্ষেত্রফল = (১/২) × কর্ণদ্বয়ের গুণফল
= (১/২) × ১৮ × ৯
= ৮১ বর্গমিটার
বর্গক্ষেত্রের ক্ষেত্রফল = ৮১ বর্গমিটার
বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য = √৮১ মিটার
= ৯ মিটার
∴ বর্গক্ষেত্রটির পরিসীমা = ৪ × ৯ মিটার
= ৩৬ মিটার
0
Updated: 2 months ago