একটি ত্রিভুজ এবং বৃত্ত ন্যুনতম কয়টি বিন্দুতে ছেদ করতে পারে ?
A
১
B
৩
C
২
D
৪
উত্তরের বিবরণ
একটি ত্রিভুজ এবং বৃত্ত ন্যূনতম ২টি বিন্দুতে ছেদ করতে পারে। কারণ, একটি ত্রিভুজ তিনটি বাহু নিয়ে গঠিত এবং প্রতিটি বাহু একটি সরলরেখা। একটি বৃত্ত কোনো সরলরেখাকে সর্বাধিক দুইটি বিন্দুতে ছেদ করতে পারে, তবে ন্যূনতম একটি বাহুর সঙ্গে ছেদ ঘটলে সেটি দুইটি বিন্দুতেই হবে। তাই ন্যূনতম ছেদবিন্দুর সংখ্যা হবে ২।
-
ত্রিভুজের বাহু তিনটি, প্রতিটি বাহু বৃত্তকে সর্বাধিক ২টি বিন্দুতে ছেদ করতে পারে।
-
যদি বৃত্তটি শুধু একটি বাহুর সঙ্গে ছেদ করে, তবে সেই ছেদ হবে ২টি বিন্দুতে।
-
কোনো বাহুর সঙ্গে বৃত্ত যদি স্পর্শক আকারে থাকে, তখন ছেদ হবে ১টি বিন্দুতে, কিন্তু প্রশ্নে “ন্যূনতম” বলা হয়েছে ত্রিভুজের ক্ষেত্রে, অর্থাৎ পুরো ত্রিভুজের জন্য সর্বনিম্ন ছেদবিন্দু বিবেচনা করতে হবে।
-
ত্রিভুজ ও বৃত্তের পারস্পরিক অবস্থান অনুযায়ী ছেদবিন্দু সংখ্যা পরিবর্তিত হতে পারে—২, ৪, ৬ ইত্যাদি—but সর্বনিম্ন মান হলো ২টি বিন্দু।
অতএব সঠিক উত্তর হলো গ) ২।
0
Updated: 16 hours ago
একটি বৃত্তের ব্যাসার্ধ যদি ৪০% কমে, তবে বৃত্তের ক্ষেত্রফল কত কমে?
Created: 2 months ago
A
৬৪%
B
৫৮%
C
৪৪%
D
৬৬%
প্রশ্ন: একটি বৃত্তের ব্যাসার্ধ যদি ৪০% কমে, তবে বৃত্তের ক্ষেত্রফল কত কমে?
সমাধান:
আমরা জানি,
বৃত্তের ক্ষেত্রফল = πr2
অর্থাৎ, বৃত্তের ব্যাসার্ধ ৪০% কমলে ২ বার ৪০% করে কমবে।
∴ প্রথম বার কমে হবে = (১০০ - ৪০)%
= ৬০%
আবার,
দ্বিতীয় বার কমবে = ৬০ এর ৪০%
= ৬০ × (৪০/১০০)
= ২৪০০/১০০
= ২৪%
∴ ক্ষেত্রফল মোট কমবে = (৪০ + ২৪)%
= ৬৪% ।
0
Updated: 2 months ago
নিচের কোন বাহুগুলো দ্বারা একটি সমকোণী ত্রিভুজ অঙ্কন করা সম্ভব?
Created: 1 month ago
A
৪, ৫, ৬
B
৭, ৮, ১০
C
৬, ৭, ৮
D
৮, ১৫, ১৭
প্রশ্ন: নিচের কোন বাহুগুলো দ্বারা একটি সমকোণী ত্রিভুজ অঙ্কন করা সম্ভব?
সমাধান:
আমরা জানি,
পিথাগোরাসের উপপাদ্য অনুসারে, একটি সমকোণী ত্রিভুজের ক্ষেত্রে অতিভুজের (বৃহত্তম বাহুর) বর্গ অপর দুই বাহুর বর্গের সমষ্টির সমান।
অপশন (ক): ৪, ৫, ৬
বৃহত্তম বাহু = ৬২ = ৩৬
অন্য দুই বাহু: ৪২ + ৫২ = ১৬ + ২৫ = ৪১
যেহেতু ৩৬ ≠ ৪১, তাই এটি সমকোণী ত্রিভুজ নয়।
অপশন (খ): ৭, ৮, ১০
বৃহত্তম বাহু = ১০২ = ১০০
অন্য দুই বাহু: ৭২ + ৮২ = ৪৯ + ৬৪ = ১১৩
যেহেতু ১০০ ≠ ১১৩, তাই এটি সমকোণী ত্রিভুজ নয়।
অপশন (গ): ৬, ৭, ৮
বৃহত্তম বাহু = ৮২ = ৬৪
অন্য দুই বাহু: ৬২ + ৭২ = ৩৬ + ৪৯ = ৮৫
যেহেতু ৬৪ ≠ ৮৫, তাই এটি সমকোণী ত্রিভুজ নয়।
অপশন (ঘ): ৮, ১৫, ১৭
বৃহত্তম বাহু = ১৭২ = ২৮৯
অন্য দুই বাহু: ৮২ + ১৫২ = ৬৪ + ২২৫ = ২৮৯
যেহেতু ২৮৯ = ২৮৯, তাই এটি সমকোণী ত্রিভুজ গঠন করা সম্ভব।
∴ সঠিক উত্তর : অপশন (ঘ)
0
Updated: 1 month ago
ত্রিভুজ ABC এর BE = EF = CF এবং ত্রিভুজ AEC এর ক্ষেত্রফল 48 বর্গফুট হলে ABC ত্রিভুজের ক্ষেত্রফল কত বর্গফুট?
Created: 1 month ago
A
48 বর্গফুট
B
60 বর্গফুট
C
64 বর্গফুট
D
72 বর্গফুট
প্রশ্ন: 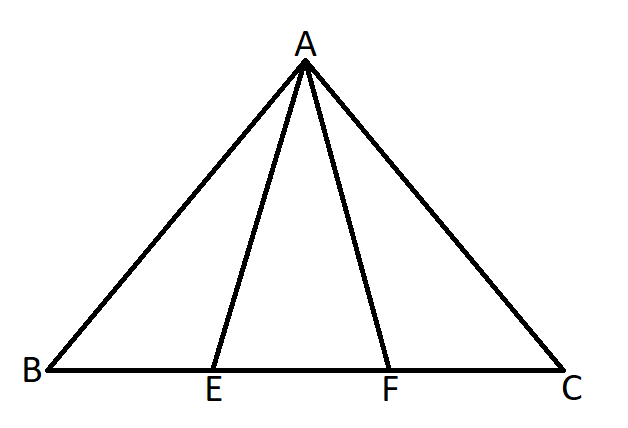
ত্রিভুজ ABC এর BE = EF = CF এবং ত্রিভুজ AEC এর ক্ষেত্রফল 48 বর্গফুট হলে ABC ত্রিভুজের ক্ষেত্রফল কত বর্গফুট?
সমাধান:
দেওয়া আছে,
AEC ত্রিভুজের ক্ষেত্রফল = 48
এবং ABC ত্রিভুজে BE = EF = CF
যেহেতু ABC ত্রিভুজে EF = CF
∴ ΔAEF = ΔAFC
এখন,
ΔAEC = 48 বর্গফুট
বা, ΔAEF + ΔAFC = 48 বর্গফুট
বা, 2 ΔAEF = 48 বর্গফুট
বা, ΔAEF = 48/2 = 24 বর্গফুট
∴ ΔAEF = ΔAFC = 24 বর্গফুট
আবার,
যেহেতু ABC ত্রিভুজে BE = EF
∴ ΔABE = ΔAEF = 24 বর্গফুট
এখন, ABC ত্রিভুজে ΔABE + ΔAEF + ΔAFC = 24 + 24 + 24 = 72 বর্গফুট
0
Updated: 1 month ago