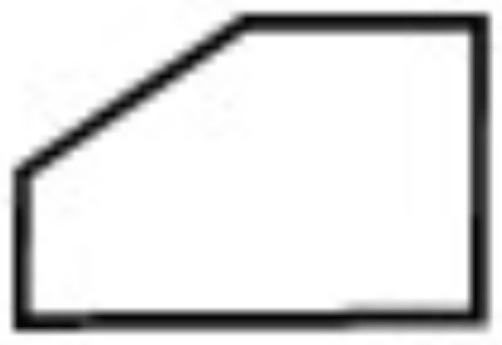
একটি সমকোণী ত্রিভুজের অতিভুজ 25 মিটার। অপর বাহুদ্বয়ের একটি অপরটির 3/4 অংশ হলে, অপর বাহুদ্বয়ের দৈর্ঘ্য অনুপাত-
A
3 : 4
B
1 : 2
C
3 : 5
D
2 : 1
উত্তরের বিবরণ
প্রশ্নঃ একটি সমকোণী ত্রিভুজের অতিভুজ ২৫ মিটার। অপর বাহুদ্বয়ের একটি অপরটির ৩/৪ অংশ হলে, অপর বাহুদ্বয়ের দৈর্ঘ্য অনুপাত নির্ণয় কর।
সমাধানঃ
ধরা যাক, অপর দুই বাহু যথাক্রমে ( x ) মিটার এবং ( \frac{3x}{4} ) মিটার।
অতিভুজ = ২৫ মিটার।
পাইথাগোরাসের সূত্র অনুযায়ী,
অতিভুজ² = প্রথম বাহু² + দ্বিতীয় বাহু²
অতএব,
( 25² = x² + \left(\frac{3x}{4}\right)² )
⇒ ( 625 = x² + \frac{9x²}{16} )
⇒ ( 625 = \frac{16x² + 9x²}{16} )
⇒ ( 625 = \frac{25x²}{16} )
⇒ ( x² = \frac{625×16}{25} )
⇒ ( x² = 400 )
⇒ ( x = 20 )
অতএব, অপর দুটি বাহু হলো ২০ মিটার এবং ( \frac{3×20}{4} = ১৫ ) মিটার।
সুতরাং, অপর বাহুদ্বয়ের দৈর্ঘ্য অনুপাত = ১৫ : ২০ = ৩ : ৪
উত্তরঃ ক) ৩ : ৪
0
Updated: 1 day ago
একটি বই 10% ক্ষতিতে বিক্রি করা হইল। বিক্রয়মূল্য 60 টাকা বেশী হলে 5% লাভ হত। বইটির ক্রয়মূল্য কত টাকা?
Created: 2 weeks ago
A
200
B
300
C
400
D
500
প্রশ্ন: একটি বই 10% ক্ষতিতে বিক্রি করা হইল। বিক্রয়মূল্য 60 টাকা বেশী হলে 5% লাভ হত। বইটির ক্রয়মূল্য কত টাকা?
সমাধান:
ধরি,
বইটির ক্রয়মূল্য = 100 টাকা
10% ক্ষতিতে, বিক্রয়মূল্য = 100 - 10 = 90 টাকা
5% লাভে, বিক্রয়মূল্য = 100 + 5 = 105 টাকা
∴ বিক্রয়মূল্য বেশি = 105 - 90 = 15 টাকা
বিক্রয়মূল্য 15 টাকা বেশি হলে ক্রয়মূল্য = 100 টাকা
বিক্রয়মূল্য 1 টাকা বেশি হলে ক্রয়মূল্য = 100/15 টাকা
বিক্রয়মূল্য 60 টাকা বেশি হলে ক্রয়মূল্য = (100 × 60)/15 টাকা
= 400 টাকা
সুতরাং, বইটির ক্রয়মূল্য 400 টাকা।
0
Updated: 2 weeks ago
নিচের কোনটি অমূলদ সংখ্যা?
Created: 1 month ago
A
B
√9 (ভুল উত্তর)
C
D
√(27/48)
প্রশ্ন: নিচের কোনটি অমূলদ সংখ্যা?
সমাধান:
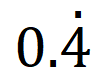= মূলদ সংখ্যা
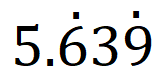= মূলদ সংখ্যা
√9 = 3 = মূলদ সংখ্যা
√(27/48) = √(9/16) = 3/4 মূলদ সংখ্যা
সঠিক উত্তর নেই। তাই প্রশ্নটি বাতিল করা হল।
অমূলদ সংখ্যা:
যে সংখ্যাকে p/q আকারে প্রকাশ করা যায় না, যেখানে p ও q পূর্ণসংখ্যা এবং q ≠ 0, সে সংখ্যাকে অমূলদ সংখ্যা বলা হয়।
- পূর্ণবর্গ নয় এরূপ যে কোনাে স্বাভাবিক সংখ্যার বর্গমূল কিংবা তার ভগ্নাংশ একটি অমূলদ সংখ্যা।
যেমন√2 = 1.414213..., √3 = 1.732 ..., √11= 3.31662............ ইত্যাদি অমূলদ সংখ্যা।
- কোনাে অমূলদ সংখ্যাকে দুইটিপূর্ণ সংখ্যার অনুপাত হিসেবে প্রকাশ করা যায় না।
- অমূলদ সংখ্যাকে একটি মূলদ সংখ্যা দ্বারা গুণ করলে অমূলদ সংখ্যা পাওয়া যায়।
0
Updated: 1 month ago
অংশগুলি জোড়া দিলে কোন চিত্র হবে?
Created: 1 month ago
A
B
C
D
অংশগুলি জোড়া দিলে অপশন খ এর চিত্র অনুরুপ।
0
Updated: 1 month ago
