দুটি ধনাত্মক সংখ্যার বর্গের অন্তর 8 গুণফল 3, সংখ্যা দুটির বর্গের সমষ্টি কত?
A
8
B
10
C
13
D
25
উত্তরের বিবরণ
প্রশ্নঃ দুটি ধনাত্মক সংখ্যার বর্গের অন্তর ৮, গুণফল ৩। সংখ্যা দুটির বর্গের সমষ্টি কত?
সমাধানঃ
ধরি, দুটি ধনাত্মক সংখ্যা ( x ) এবং ( y )।
তাহলে,
( x^2 - y^2 = 8 ) … (১)
এবং ( xy = 3 ) … (২)
সমীকরণ (১) থেকে পাই,
( (x + y)(x - y) = 8 )
এখন,
আমরা জানি,
( (x + y)^2 = x^2 + 2xy + y^2 )
অতএব,
( x^2 + y^2 = (x + y)^2 - 2xy )
এখন ( x + y ) এবং ( x - y )-এর মান বের করতে হবে।
ধরি, ( x + y = a ) এবং ( x - y = b )
তাহলে, ( ab = 8 ) এবং ( xy = 3 )
এখন,
( x = \dfrac{a + b}{2} ) এবং ( y = \dfrac{a - b}{2} )
তাহলে,
( xy = \dfrac{(a + b)(a - b)}{4} = \dfrac{a^2 - b^2}{4} )
অতএব,
( \dfrac{a^2 - b^2}{4} = 3 )
⇒ ( a^2 - b^2 = 12 ) … (৩)
আবার (১) অনুযায়ী, ( ab = 8 )
এখন, (৩) থেকে পাই,
( a^2 + b^2 = (a^2 - b^2) + 2b^2 = 12 + 2b^2 )
কিন্তু আমাদের প্রয়োজন ( x^2 + y^2 = \dfrac{a^2 + b^2}{2} )
তাহলে,
( x^2 + y^2 = \dfrac{12 + 2b^2}{2} = 6 + b^2 )
এখন, ( ab = 8 ) ⇒ ( a = \dfrac{8}{b} )
(৩) থেকে, ( a^2 - b^2 = 12 )
অর্থাৎ, ( \dfrac{64}{b^2} - b^2 = 12 )
⇒ ( 64 - b^4 = 12b^2 )
⇒ ( b^4 + 12b^2 - 64 = 0 )
ধরি, ( b^2 = k )
তাহলে, ( k^2 + 12k - 64 = 0 )
অতএব,
( k = \dfrac{-12 ± \sqrt{12^2 - 4×1×(-64)}}{2} = \dfrac{-12 ± \sqrt{144 + 256}}{2} = \dfrac{-12 ± \sqrt{400}}{2} = \dfrac{-12 ± 20}{2} )
অতএব, ( k = 4 ) (ধনাত্মক মান গ্রহণ করব)
অতএব, ( b^2 = 4 )
এখন, ( x^2 + y^2 = 6 + b^2 = 6 + 4 = 10 )
উত্তরঃ ১০
0
Updated: 1 day ago
x+(2/x) = 3 হলে x³+(8/x³) = কত?
Created: 1 day ago
A
16
B
9
C
8
D
0
প্রশ্নঃ x + (2/x) = 3 হলে x³ + (8/x³) = কত?
সমাধানঃ
প্রদত্ত,
x + (2/x) = 3
এখন দুই পাশের ঘন করলে পাই,
(x + 2/x)³ = 3³
অর্থাৎ,
x³ + (8/x³) + 3x × (2/x) × (x + 2/x) = 27
অতএব,
x³ + (8/x³) + 3×2×3 = 27
⇒ x³ + (8/x³) + 18 = 27
অতএব,
x³ + (8/x³) = 27 - 18
= 9
উত্তরঃ খ) 9
0
Updated: 1 day ago
চিত্রে ∠PQR = 55°, ∠LRN = 90° এবং PQ || MR, PQ = PR হলে, ∠NRP এর মান নিচের কোনটি?
Created: 1 month ago
A
90°
B
55°
C
45°
D
35°
প্রশ্ন: চিত্রে ∠PQR = 55°, ∠LRN = 90° এবং PQ || MR, PQ = PR হলে, ∠NRP এর মান নিচের কোনটি?
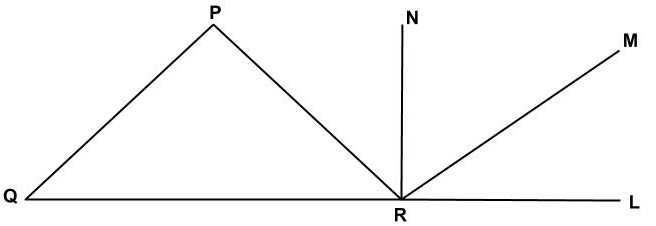
সমাধান:
প্রদত্ত চিত্রে,
PQ = PR
সুতরাং, PQR সমদ্বিবাহু ত্রিভুজ।
∠PQR = ∠PRQ = 55°
∠LRN = 90° হলে ∠NRQ = 90°
সুতরাং, ∠NRP = ∠NRQ - ∠PRQ = 90° - 55° = 35°
0
Updated: 1 month ago
মূল বিন্দু হতে (-5, 5) এবং (5, k) বিন্দুদ্বয়ের দুরত্ব সমান হতে k এর মান কত?
Created: 1 day ago
A
0
B
3
C
4
D
5
প্রশ্নঃ মূল বিন্দু হতে (-5, 5) এবং (5, k) বিন্দুদ্বয়ের দুরত্ব সমান হতে k এর মান কত?
সমাধানঃ
ধরা যাক, মূল বিন্দু O(0, 0)।
প্রথম বিন্দু A(-5, 5)
দ্বিতীয় বিন্দু B(5, k)
এখন,
O থেকে A পর্যন্ত দূরত্ব = √[(-5 - 0)² + (5 - 0)²]
= √[(−5)² + 5²]
= √(25 + 25)
= √50
O থেকে B পর্যন্ত দূরত্ব = √[(5 - 0)² + (k - 0)²]
= √(25 + k²)
যেহেতু দুটি দূরত্ব সমান,
√50 = √(25 + k²)
উভয় পাশে বর্গ করলে,
50 = 25 + k²
অতএব,
k² = 50 − 25
= 25
সুতরাং,
k = ±5
অতএব, k = 5
উত্তরঃ ঘ) 5
0
Updated: 1 day ago