২৮ ডিগ্রি কোণের সম্পূরক কোণের পরিমাণ কত?
A
৬২ ডিগ্রি
B
১১৮ ডিগ্রি
C
৩৩২ ডিগ্রি
D
১৫২ ডিগ্রি
উত্তরের বিবরণ
কোনো কোণ এবং তার সম্পূরক কোণ সম্পর্কে মূল ধারণা হলো, দুটি কোণের যোগফল সবসময় ১৮০° হয়। অর্থাৎ, যদি কোনো কোণ জানা থাকে, তাহলে তার সম্পূরক কোণ বের করতে আমরা ১৮০° থেকে সেই কোণটি বিয়োগ করি। এই সূত্রটি খুবই সরল ও প্রাথমিক জ্যামিতির নিয়মের অন্তর্ভুক্ত।
দেওয়া উদাহরণে, মূল কোণ হলো ২৮°। সম্পূরক কোণ বের করার জন্য আমরা ১৮০° থেকে ২৮° বিয়োগ করব:
১৮০° − ২৮° = ১৫২°
এখানেই আমরা পাই উত্তর ১৫২°, যা প্রদত্ত বিকল্পগুলোর মধ্যে ঘ)। এটি দেখায় যে, ২৮° কোণের সঙ্গে যে কোণটি মিলে একসাথে ১৮০° হয়, সেটি সম্পূর্ণরূপে ১৫২°।
এখন কিছু গুরুত্বপূর্ণ বিষয়, যা বোঝা জরুরি:
-
সম্পূরক কোণ বলতে দুটি কোণকে বোঝায় যেগুলোর যোগফল ১৮০°। এটি সাধারণত সোজা কোণ সম্পর্কিত গণনায় ব্যবহার হয়।
-
যেকোনো কোণ X° হলে, তার সম্পূরক কোণ হবে (১৮০° − X°)।
-
উদাহরণ হিসেবে, যদি কোনো কোণ ৯০° হয়, তার সম্পূরক কোণও ৯০° হবে, কারণ ৯০° + ৯০° = ১৮০°।
-
সম্পূরক কোণ শুধুমাত্র প্রথম কোণের সাথে মিলে ১৮০° তৈরি করার জন্য প্রয়োজন, এটি সাধারণত ত্রিভুজ বা বিভিন্ন জ্যামিতিক সমস্যা সমাধানে কাজে আসে।
-
এই নিয়মটি কোণ সংক্রান্ত বিভিন্ন জ্যামিতিক হিসাব যেমন ত্রিভুজের অভ্যন্তরীণ কোণ, বাহ্যিক কোণ বা সমকোণীয় চিত্র বিশ্লেষণে সাহায্য করে।
সুতরাং, ২৮° কোণের সম্পূরক কোণ গণনা করা খুব সরল প্রক্রিয়া: মূল কোণটিকে ১৮০° থেকে বিয়োগ করলে তা পাওয়া যায়। এভাবে আমরা নিশ্চিত করতে পারি যে দুটি কোণের যোগফল সঠিকভাবে ১৮০° হয়েছে।
এটি মূলত শুধু একটি সরল সূত্রের প্রয়োগ, যা সমস্ত প্রাথমিক জ্যামিতি সমস্যায় ব্যবহারযোগ্য। তাই, ২৮° কোণের সম্পূরক কোণ সবসময় ১৫২°, এবং প্রদত্ত বিকল্পের মধ্যে ঘ) সঠিক উত্তর।
এই ধরনের হিসাব শিক্ষার্থীদের কোণ সংক্রান্ত ধারণা শক্তিশালী করতে সাহায্য করে এবং বিভিন্ন জ্যামিতিক সমস্যা সমাধানে সহজীকরণ নিয়ে আসে।
0
Updated: 4 days ago
একটি
25 মিটার লম্বা মই দেয়ালের সাথে
খাড়া করে রাখা আছে।
মইটির গোড়া দেয়াল থেকে কত দূরে
সরালে এর উপরের অংশ
5 মিটার নিচে নেমে আসবে?
Created: 1 month ago
A
13 মিটার
B
10 মিটার
C
18 মিটার
D
15 মিটার
প্রশ্ন: একটি 25 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 5 মিটার নিচে নেমে আসবে?
সমাধান:
এখানে, AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত A বিন্দু থেকে B বিন্দুতে 5 মিটার নামবে।
মইয়ের দৈর্ঘ্য, AC = BD = 25 মিটার
এবং AB = 5 মিটার
∴ BC = 25 - 5 = 20 মিটার
এখন, পিথাগোরাসের সূত্র অনুযায়ী পাই,
BD2 = BC2 + CD2
⇒ 252 = 202 + CD2
⇒ 625 = 400 + CD2
⇒ CD2 = 625 - 400
⇒ CD2 = 225
⇒ CD = √225
⇒ CD = 15 মিটার
∴ মইটির গোড়া দেয়াল থেকে 15 মিটার দূরে সরালে এর উপরের অংশ 5 মিটার নিচে নেমে আসবে।
0
Updated: 1 month ago
একটি ট্রাপিজিয়ামের ক্ষেত্রফল ২৫ বর্গফুট। যদি উচ্চতা ২ ফুট এবং সমান্তরাল বাহুদুইটি একটি অপরটির থেকে ১ ফুট বেশি হলে বড় বাহুটির দৈর্ঘ্য কত?
Created: 2 months ago
A
১০ ফুট
B
১২ ফুট
C
১৩ ফুট
D
২৫ ফুট
প্রশ্ন: একটি ট্রাপিজিয়ামের ক্ষেত্রফল ২৫ বর্গফুট। যদি উচ্চতা ২ ফুট এবং সমান্তরাল বাহুদুইটি একটি অপরটির থেকে ১ ফুট বেশি হলে বড় বাহুটির দৈর্ঘ্য কত?
সমাধান:
মনে করি,
বড় বাহুর দৈর্ঘ্য = ক ফুট
∴ ছোট বাহুর দৈর্ঘ্য = (ক - ১) ফুট
দেওয়া আছে,
উচ্চতা = ২ ফুট
ক্ষেত্রফল = ২৫ বর্গফুট
প্রশ্নমতে,
(১/২) × উচ্চতা × {ক + (ক - ১)} = ২৫
⇒ (১/২) × ২ × (২ক - ১) = ২৫
⇒ ২ক - ১ = ২৫
⇒ ২ক = ২৫ + ১
⇒ ২ক = ২৬
⇒ ক = ২৬/২
⇒ ক = ১৩
অর্থাৎ বড় বাহুটির দৈর্ঘ্য = ১৩ ফুট
0
Updated: 2 months ago
2 সে. মি. ব্যাসার্ধবিশিষ্ট একটি বৃত্তের অন্তঃস্থ একটি বর্গক্ষেত্রের চারটি বাহু এবং বৃত্তটি দ্বারা আবদ্ধ অঞ্চলের ক্ষেত্রফল কত বর্গ সে.মি.?
Created: 2 months ago
A
4π - 8
B
4π + 8
C
2π - 4
D
2π + 4
প্রশ্ন: 2 সে.মি. ব্যাসার্ধ বিশিষ্ট একটি বৃত্তের অন্তঃস্থ একটি বর্গক্ষেত্রের বহিঃস্থ এবং বৃত্তটি দ্বারা আবৃদ্ধ অঞ্চলের ক্ষেত্রফল কত বর্গ সেন্টিমিটার?
সমাধান:
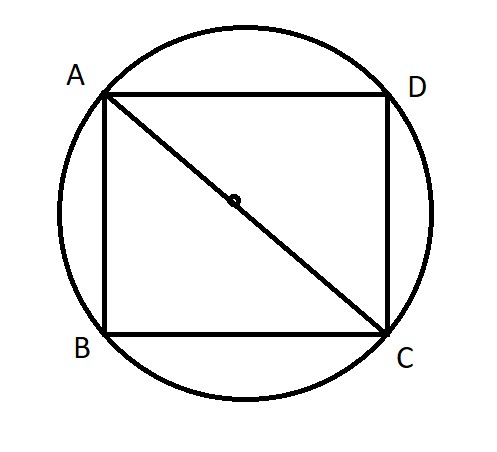
মনেকরি
বৃত্তের ব্যাসার্ধ r = 2 সে.মি
বৃত্তের ক্ষেত্রফল = πr2 = π × 22 বর্গ সে.মি
=4π বর্গ সে.মি
আবার
ABCD এ AC = 4 সে.মি.
আমরা জানি
AC2 = AB2 + BC2
⇒ AB2 + AB2 = AC2
⇒ 2AB2 = 42
⇒ 2AB2 =16
∴ AB2 = 8
বর্গক্ষেত্রের বহিঃস্থ এবং বৃত্তটি দ্বারা আবৃদ্ধ অঞ্চলের ক্ষেত্রফল = 4π - 8 বর্গ সে.মি
0
Updated: 2 months ago