x³-5x+6 < 0 এর সমাধান-
A
2 ≤ x < 3
B
2 < x < 3
C
2 < x ≤ 3
D
2 ≤ x ≤ 3
উত্তরের বিবরণ
সমাধান:
প্রথমে, সমীকরণ এর মূল খুঁজে বের করি।
সাধারণ ফ্যাক্টরিং পদ্ধতিতে:
তাহলে মূলগুলো:
ইনটেরভাল টেস্ট:
মূলগুলো ক্রমান্বয়ে সাজাই:
-
(নেতিবাচক)
-
(ধনাত্মক)
-
(নেতিবাচক)
-
(ধনাত্মক)
প্রশ্নে , অর্থাৎ নেতিবাচক।
নেতিবাচক অংশ:
উত্তর (দেওয়া অপশনের মধ্যে):
দ্রষ্টব্য: মূল যাচাই অনুযায়ী, মূলটি হলে সমীকরণ শূন্য, তাই strict inequality অনুযায়ী হলে সমাধান থাকবে।
উত্তর: 2 < x < 3
0
Updated: 4 days ago
x2 - 7x + 10 < 0 হলে, নিচের কোনটি সঠিক?
Created: 1 month ago
A
1 < x < 6
B
x > 5 অথবা x < 2
C
3 < x < 4
D
2 < x < 5
গণিত
অসমতা (Inequality)
বীজগণিত (Algebra)
সরল সমীকরণ (Simple/linear equation)
সরলীকরণ (Simplification)
প্রশ্ন: x2 - 7x + 10 < 0 হলে, নিচের কোনটি সঠিক?
সমাধান:
x2 - 7x + 10 < 0
⇒ x2 - 5x - 2x + 10 < 0
⇒ x(x - 5) - 2(x - 5) < 0
⇒ (x - 2)(x - 5) < 0
দুটি রাশির গুণফল ঋণাত্মক (শূন্যের চেয়ে ছোট) হওয়ার জন্য একটি রাশি ধনাত্মক এবং অন্যটি ঋণাত্মক হতে হবে।
ক্ষেত্র ১: (x - 2) > 0 এবং (x - 5) < 0
⇒ x > 2 এবং x < 5
⇒ 2 < x < 5
ক্ষেত্র ২: (x - 2) < 0 এবং (x - 5) > 0
⇒ x < 2 এবং x > 5
এই সম্পর্কটি একসাথে সত্য হতে পারে না।
সুতরাং, সঠিক সমাধান হলো 2 < x < 5
0
Updated: 1 month ago
x2 - y2 + 2y - 1 এর একটি উৎপাদক -
Created: 3 weeks ago
A
(x + y - 1) (x - y + 1)
B
(x + y + 1) (x - y + 1)
C
(x + y - 1) (x + y + 1)
D
(x - y - 1) (x - y + 1)
প্রশ্ন: x2 - y2 + 2y - 1 এর একটি উৎপাদক -
সমাধান:
x2 - y2 + 2y - 1
= x2 - (y2 - 2y + 1)
= x2 - (y - 1)2
= (x + y - 1) (x - y + 1)
0
Updated: 3 weeks ago
সমাধান নির্ণয় করুন-
Created: 5 months ago
A
10
B
4/3
C
15
D
12
প্রশ্ন: সমাধান নির্ণয় করুন-
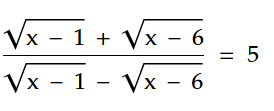
সমাধান:
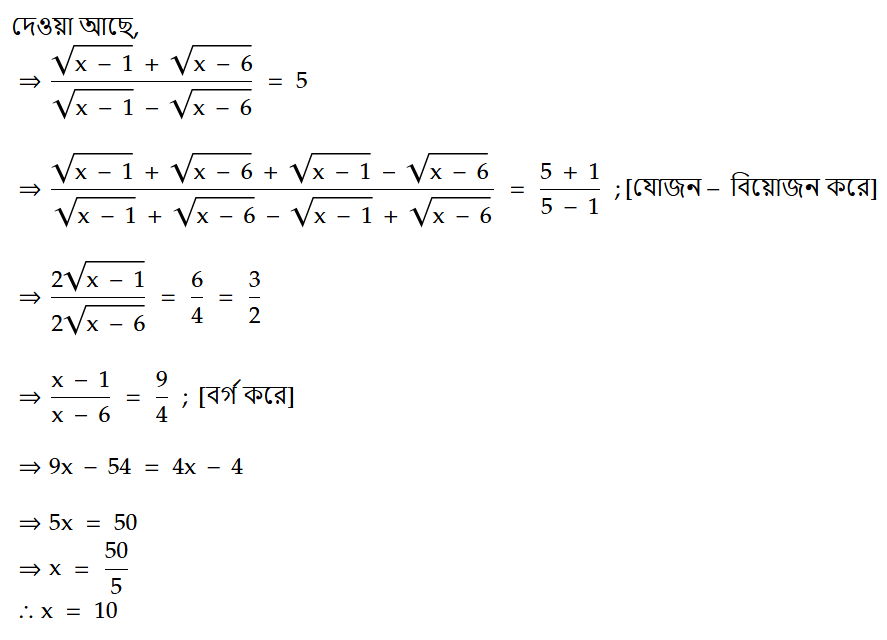
0
Updated: 5 months ago