City B is 5 miles east of city A. City C is 10 miles southeast of city B. Which of the following is the closest to the distance from city A to City C?
A
11 miles
B
12 miles
C
13 miles
D
14 miles
উত্তরের বিবরণ
Question: City B is 5 miles east of city A. City C is 10 miles southeast of city B. Which of the following is the closest to the distance from city A to City C?
Solution: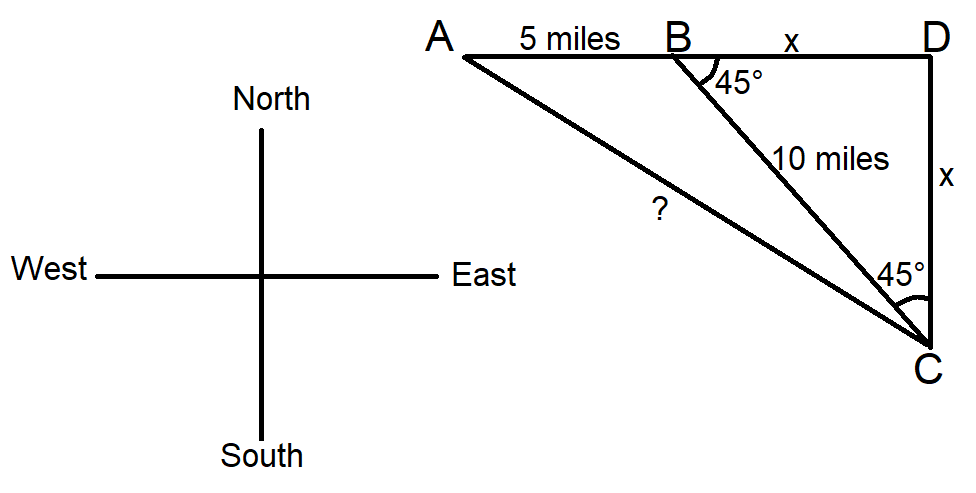
BD এবং DC দুটো সমান যেহেতু বিপরীত কোন দুইটাই 45°
অর্থাৎ, BDC ত্রিভুজ থেকে আমরা পাই,
BC2 = BD2 + DC2
⇒ 102 = x2 + x2
⇒ 2x2 = 100
⇒ x2 = 50
∴ x = 5√2
অনুরূপে, ADC থেকে পাই,
AC2 = AD2 + DC2
⇒ AC2 = (5 + x)2 + x2
= 52 + 2 · 5 · x + x2 + x2
= 25 + 10 · 5√2 + (5√2)2 + (5√2)2
= 25 + 50√2 + 50 + 50
= 125 + 50√2
= 125 + 70.71
= 195.71
∴ AC = √195.71 = 13.99
≈ 14 miles
অর্থাৎ, A থেকে C এর নিকটবর্তী দূরত্ব 14 মাইল।
0
Updated: 3 months ago
একটি মাঠের দৈর্ঘ্য ৬০ মিটার এবং প্রস্থ ৪০ মিটার। এর ভিতরে চারদিকে ৪ মিটার প্রশস্ত রাস্তা থাকলে, রাস্তার ক্ষেত্রফল কত?
Created: 2 months ago
A
৭৩৬ বর্গ মিটার
B
৮১২ বর্গ মিটার
C
৬৬৪ বর্গ মিটার
D
৯৬০ বর্গ মিটার
প্রশ্ন: একটি মাঠের দৈর্ঘ্য ৬০ মিটার এবং প্রস্থ ৪০ মিটার। এর ভিতরে চারদিকে ৪ মিটার প্রশস্ত রাস্তা থাকলে, রাস্তার ক্ষেত্রফল কত?
সমাধান:
দেওয়া আছে,
দৈর্ঘ্য = ৬০ মিটার
প্রস্থ = ৪০ মিটার
∴ ক্ষেত্রফল = ৬০ × ৪০ = ২৪০০ বর্গ মিটার
আবার,
রাস্তা বাদে,
নতুন দৈর্ঘ্য = ৬০ - (২ × ৪) = ৫২ মিটার
নতুন প্রস্থ = ৪০ - (২ × ৪) = ৩২ মিটার
∴ নতুন ক্ষেত্রফল = ৫২ × ৩২ = ১৬৬৪ বর্গ মিটার
∴ রাস্তার ক্ষেত্রফল = ২৪০০ - ১৬৬৪ = ৭৩৬ বর্গ মিটার
0
Updated: 2 months ago
সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য যদি 'a' হয় তবে ক্ষেত্রফল হবে -
Created: 5 months ago
A
(√৩a2)/৪
B
(√৩a2)/2
C
৩/(২a2)
D
√১/(২a2)
প্রশ্ন: সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য যদি 'a' হয়, তবে ক্ষেত্রফল হবে -
সমাধান:
সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a হলে ত্রিভুজটির ক্ষেত্রফল = √3a2/4
0
Updated: 5 months ago
2 সে. মি. ব্যাসার্ধবিশিষ্ট একটি বৃত্তের অন্তঃস্থ একটি বর্গক্ষেত্রের চারটি বাহু এবং বৃত্তটি দ্বারা আবদ্ধ অঞ্চলের ক্ষেত্রফল কত বর্গ সে.মি.?
Created: 2 months ago
A
4π - 8
B
4π + 8
C
2π - 4
D
2π + 4
প্রশ্ন: 2 সে.মি. ব্যাসার্ধ বিশিষ্ট একটি বৃত্তের অন্তঃস্থ একটি বর্গক্ষেত্রের বহিঃস্থ এবং বৃত্তটি দ্বারা আবৃদ্ধ অঞ্চলের ক্ষেত্রফল কত বর্গ সেন্টিমিটার?
সমাধান:
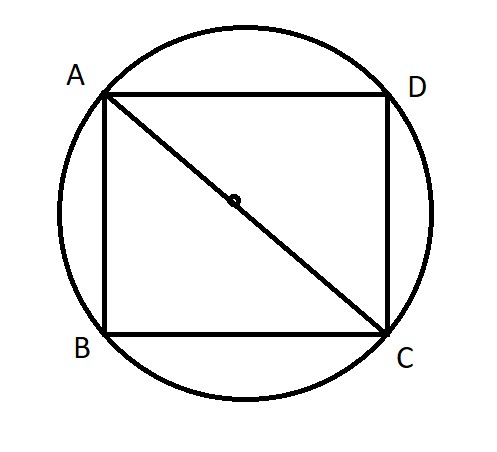
মনেকরি
বৃত্তের ব্যাসার্ধ r = 2 সে.মি
বৃত্তের ক্ষেত্রফল = πr2 = π × 22 বর্গ সে.মি
=4π বর্গ সে.মি
আবার
ABCD এ AC = 4 সে.মি.
আমরা জানি
AC2 = AB2 + BC2
⇒ AB2 + AB2 = AC2
⇒ 2AB2 = 42
⇒ 2AB2 =16
∴ AB2 = 8
বর্গক্ষেত্রের বহিঃস্থ এবং বৃত্তটি দ্বারা আবৃদ্ধ অঞ্চলের ক্ষেত্রফল = 4π - 8 বর্গ সে.মি
0
Updated: 2 months ago