প্রশ্ন: একটি কম্পিউটার সিস্টেমে (11001011)2 বাইনারি সংখ্যাটির মান ডেসিমেল এ কত হবে?

একটি কম্পিউটার সিস্টেমে ৮-বিট বাইনারি সংখ্যা (11001011)2 এর মান নির্ভর করে আমরা কীভাবে তা ইন্টারপ্রেট করি তার ওপর। যদি এটি Unsigned সংখ্যা হিসেবে ধরা হয়, তাহলে সব বিটই ধনাত্মক অবদান রাখে এবং দশমিক মান হবে 128 + 64 + 0 + 0 + 8 + 0 + 2 + 1 = 203, অর্থাৎ অপশন (গ)।

তবে, যদি আমরা এটিকে Signed Two’s Complement হিসেবে ধরি, তাহলে প্রথম বিট (MSB) = 1 হওয়ায় সংখ্যা ঋণাত্মক। Two’s complement বের করতে প্রথমে বিটগুলো উল্টে 00110100 পাই এবং ১ যোগ করলে 00110101 হয়, যার দশমিক মান = 53, সুতরাং Signed হিসেবে মান = - 53, অর্থাৎ অপশন (খ)।

অন্যদিকে, One’s Complement অনুযায়ী, MSB = 1 → ঋণাত্মক, এবং বিটগুলো উল্টে 00110100 পাওয়া যায়, যার দশমিক মান = 52, অর্থাৎ মান = - 52, অর্থাৎ অপশন (ক)।

তাই প্রাসঙ্গিক প্রসঙ্গে, একই বাইনারি সংখ্যা Unsigned, Signed Two’s Complement, বা One’s Complement হিসেবে ভিন্ন ভিন্ন মান দিতে পারে, এবং প্রদত্ত অপশন অনুযায়ী সবকটি মান সম্ভব।

- একই ৮-বিট সংখ্যা (11001011)2 এর জন্য Unsigned = 203, Two’s Complement Signed = -53, One’s Complement Signed = - 52

[উল্লেখ্য, PSC অপশন (ঘ) তে সচরারচর - "উপরের সবকটি" দিয়ে থাকে, কিন্তু ৪৭ তম বিসিএসে এবার অপশন (ঘ) - "উপরের সবকটি হতে পারে" দিয়েছে। সব ছোট বিষয়ও খেয়াল রেখে উত্তর করতে হবে।] 

বিস্তারিত সমাধান

১. যদি Unsigned সংখ্যা হিসেবে ধরা হয়:
(11001011)2 = (1 × 27) + (1 × 26) + (0 × 25) + (0 × 24) + (1 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 128 + 64 + 0 + 0 + 8 + 0 + 2 + 1 = 203
অতএব, Unsigned হলে মান = 203

২. যদি Signed (Two’s Complement, 8-bit) সংখ্যা হিসেবে ধরা হয়:
- প্রথম বিট = 1 → সংখ্যা নেগেটিভ।
- Two’s complement বের করতে: প্রথমে বিট ইনভার্ট → 00110100
- তারপর 1 যোগ করলে → 00110101 = 53
অতএব, Signed হলে মান = - 53

- Unsigned interpretation: 203
- Signed interpretation: - 53

(৩) One’s Complement নিয়ম (8-bit):

MSB = 1 → সংখ্যা ঋণাত্মক। 
Magnitude = Bitwise complement (বিটের উল্টো)

⇒ 8-bit সংখ্যা 110010112

⇒ MSB = 1 → সংখ্যা ঋণাত্মক। 

⇒ Bitwise complement: 
11001011 → 001101002

⇒ 001101002 এর দশমিক মান = 52

⇒  অতএব, One’s Complement অনুযায়ী এই সংখ্যার মান = -52 (অপশন ক)

উল্লেখ্য,
- MSB এর পূর্ণরূপ হলো: Most Significant Bit.
- এটি একটি বাইনারি সংখ্যার সবচেয়ে গুরুত্বপূর্ণ বিট।
- সাধারণত, MSB সংখ্যা নির্ধারণ করে যে সংখ্যা ধনাত্মক না ঋণাত্মক (Signed Binary Number) বা বাইনারি সংখ্যার সর্বোচ্চ মানের অংশ।
(11001011)2
এখানে, প্রথম 1 = MSB

Signed 8-bit Two’s Complement এ MSB = 1 → সংখ্যা ঋণাত্মক
MSB = 0 → সংখ্যা ধনাত্মক। 

◉ একটি অক্টাল সংখ্যাকে বাইনারিতে রূপান্তর করলে প্রতি অঙ্কের জন্য ৩টি বাইনারি বিট লাগে।
উদাহরণস্বরূপ:
অক্টাল 7 = বাইনারি 111
অক্টাল 5 = বাইনারি 101

সুতরাং, বাইনারি থেকে অক্টাল রূপান্তরের সময় প্রতি ৩টি বাইনারি বিট = ১টি অক্টাল ডিজিট। এজন্য ৩টি বাইনারি ডিজিট একসাথে গ্রুপ করা হয়।

বাইনারি থেকে অক্ট্যাল রূপান্তর: 
- একটি অক্ট্যাল সংখ্যা তিন বিট বাইনারি দ্বারা প্রকাশ করা যায়।
- আমরা জানি, বাইনারি সংখ্যার ভিত্তি ২ এবং অক্ট্যাল সংখ্যার ভিত্তি ৮।
- বাইনারি সংখ্যাকে অক্টালে রূপান্তর করতে সংখ্যাটির অংকগুলোকে তিন বিট বিশিষ্ট ছোট ছোট ভাগে ভাগ করা হয়।
- এরপর প্রতিটি গ্রুপের সমতুল্য অক্ট্যাল মান বসালে তা বাইনারি থেকে অক্টালে রূপান্তরিত হয়।

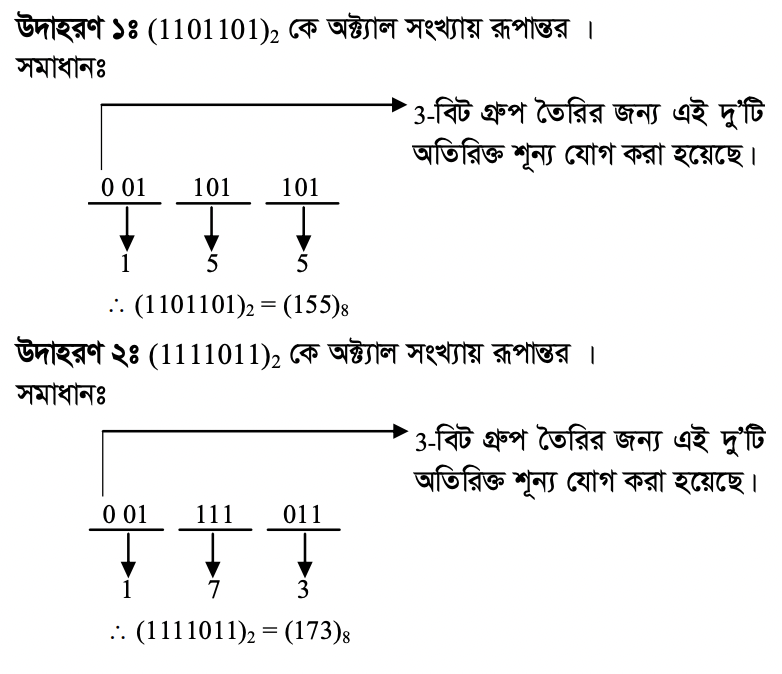
উৎস: 

হেক্সাডেসিমাল → বাইনারি রূপান্তর

ধাপসমূহ:

1. হেক্সাডেসিমেল সংখ্যা $(12A)_{16}$ লিখো।

2. প্রতিটি হেক্সাডেসিমেল অঙ্ককে ৪-বিট বাইনারি হিসেবে রূপান্তর করো:

   $$1 \to 0001, \quad 2 \to 0010, \quad A \to 1010$$

3. সবগুলো মিলিয়ে লেখো:

   $$0001\ 0010\ 1010 = 100101010$$

উপসংহার:

$$(12A)_{16} = (100101010)_2$$

উৎস:
তথ্য ও যোগাযোগ প্রযুক্তি, একাদশ ও দ্বাদশ শ্রেণি, প্রকৌশলী মুজিবুর রহমান