প্রশ্ন: ৮ সে.মি. ব্যাসার্ধ বিশিষ্ট বৃত্তের অন্তর্লিখিত বর্গক্ষেত্রের ক্ষেত্রফল কত?

সমাধান:
বৃত্তের ব্যাস = ব্যাসার্ধ × ২ = (৮ × ২) = ১৬ সেমি

আমরা জানি,
বৃত্তের অন্তর্লিখিত বর্গক্ষেত্রের কর্ণ বৃত্তের ব্যাসের সমান।

ধরি,
বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য = ক সে.মি.
∴ কর্ণের দৈর্ঘ্য = √২ × ক সে.মি.

প্রশ্নমতে,
√২ × ক = ১৬
⇒ ক = ১৬/√২

∴ বর্গক্ষেত্রটির ক্ষেত্রফল = (১৬/√২)২ বর্গ সে.মি.
= ২৫৬/২ = ১২৮ বর্গ সে.মি.

 ∴ বৃত্তের অন্তর্লিখিত বর্গক্ষেত্রের ক্ষেত্রফল = ১২৮ বর্গ সে.মি.।

প্রশ্ন: বার্ষিক শতকরা 10 টাকা মুনাফায় 5000 টাকার 3 বছরের সরল মুনাফা ও চক্রবৃদ্ধি মুনাফার পার্থক্য কত হবে?

সমাধান:
দেওয়া আছে,
আসল, p = 5000 টাকা 
সময়, n = 3 বছর 
মুনাফার হার, r = 10% 

আমরা জানি,
চক্রবৃদ্ধি মুনাফা
= p(1 + r)n - p
= 5000 × {1 + (10/100)}3 - 5000
= 5000 × {1 + (1/10)}3 - 5000
= 5000 × {(10 + 1)/10}3 - 5000
= 5000 × (11/10)3 - 5000
= 5000 × {(1331/1000) - 1}
= 5000 × {(1331 - 1000)/1000}
= 5000 × (331/1000)
= 1655

এবং , সরল মুনাফা
= pnr/১০০
= (5000 × 3 × 10)/100
= 500 × 3
=1500

∴ পার্থক্য = চক্রবৃদ্ধি মুনাফা - সরল মুনাফা
= 1655 - 1500
= 155

প্রশ্ন: একটি 20 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 4 মিটার নিচে নেমে আসবে?

সমাধান: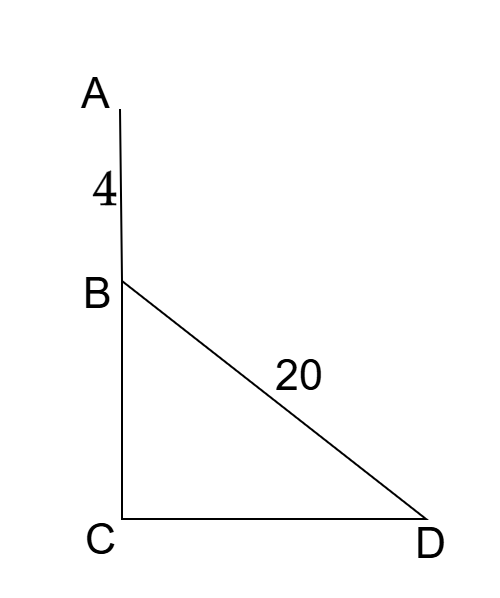


এখানে, AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত A বিন্দু থেকে B বিন্দুতে 4 মিটার নামবে। মইয়ের দৈর্ঘ্য, AC = BD = 20 মিটার 
এবং AB = 4 মিটার, BC = 20 - 4 = 16 মিটার 

এখন, পীথাগোরাসের সূত্র অনুযায়ী,
BC2 + CD2 = BD2
⇒ CD2 = BD2 - BC2
⇒ CD2 = 202 - 162
⇒ CD2 = 400 - 256
⇒ CD2 = 144
⇒ CD = √144
∴ CD = 12

∴ মইটির গোড়া দেয়াল থেকে 12 মিটার দূরে সরালে উপরের প্রান্ত 4 মিটার নিচে নামবে।