(5,6) কেন্দ্রবিশিষ্ট বৃত্ত y-অক্ষকে স্পর্শ করলে, বৃত্তটির ব্যাস কত একক?
A
5 একক
B
6 একক
C
10 একক
D
12 একক
উত্তরের বিবরণ
সমাধান:
কেন্দ্র (5,6) বিশিষ্ট একটি বৃত্ত যদি y-অক্ষকে স্পর্শ করে (অর্থাৎ x = 0), তাহলে কেন্দ্র থেকে y-অক্ষ পর্যন্ত অনুভূমিক দূরত্বই বৃত্তের ব্যাসার্ধ।
কেন্দ্রের X-সমন্বয় = 5 = দূরত্ব = |5| = 5 একক
তাহলে ব্যাসার্ধ = 5 একক
⇒ ব্যাস = 2 × 5 একক
⇒ ব্যাস = 10 একক
∴ বৃত্তটির ব্যাস = 10 একক
কেন্দ্র (5,6) বিশিষ্ট একটি বৃত্ত যদি y-অক্ষকে স্পর্শ করে (অর্থাৎ x = 0), তাহলে কেন্দ্র থেকে y-অক্ষ পর্যন্ত অনুভূমিক দূরত্বই বৃত্তের ব্যাসার্ধ।
কেন্দ্রের X-সমন্বয় = 5 = দূরত্ব = |5| = 5 একক
তাহলে ব্যাসার্ধ = 5 একক
⇒ ব্যাস = 2 × 5 একক
⇒ ব্যাস = 10 একক
∴ বৃত্তটির ব্যাস = 10 একক
0
Updated: 15 hours ago
ABCD is a square and one of its sides AB is also a chord of the circle as shown in the figure. What is the area of the square?
Created: 2 weeks ago
A
12
B
9
C
12√2
D
18
Question: ABCD is a square and one of its sides AB is also a chord of the circle as shown in the figure. What is the area of the square?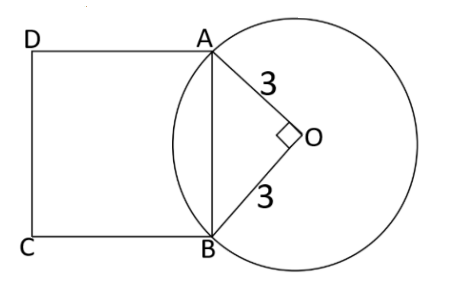
Solution:
চিত্রানুসারে, O হলো বৃত্তের কেন্দ্র এবং OA ও OB হলো বৃত্তের ব্যাসার্ধ, যার দৈর্ঘ্য 3।
AOB একটি সমকোণী ত্রিভুজ, যেখানে ∠AOB = 90° এবং অতিভুজ = AB
পিথাগোরাসের উপপাদ্য অনুসারে,
AB2 = OA2 + OB2
AB2 = 32 + 32
AB2 = 9 + 9
AB2 = 18
আমরা জানি, বর্গক্ষেত্রের ক্ষেত্রফল = বাহুর দৈর্ঘ্য২
যেহেতু ABCD একটি বর্গ, তাই এর ক্ষেত্রফল হলো AB2
সুতরাং, বর্গটির ক্ষেত্রফল হলো 18
0
Updated: 2 weeks ago
যদি একটি বৃত্তের ব্যাসার্ধ 1 সে.মি. বাড়ানো হয়, তবে এটির ক্ষেত্রফল 22 বর্গ সেমি. বাড়ে। বৃত্তটির প্রকৃত ব্যাসার্ধ কত?
Created: 15 hours ago
A
3 cm
B
3.6 cm
C
4 cm
D
4.8 cm
সমাধান:
ধরি, বৃত্তটির প্রকৃত ব্যাসার্ধ = r সে.মি.
শর্তমতে,
π[(r + 1)2 - r2] = 22
⇒ r2 + 2r + 1 - r2 = 22/ π
⇒ (2r + 1) = 22 × (7/22)
⇒ 2r + 1 = 7
⇒ 2r = 6
∴ r = 3 cm.
ধরি, বৃত্তটির প্রকৃত ব্যাসার্ধ = r সে.মি.
শর্তমতে,
π[(r + 1)2 - r2] = 22
⇒ r2 + 2r + 1 - r2 = 22/ π
⇒ (2r + 1) = 22 × (7/22)
⇒ 2r + 1 = 7
⇒ 2r = 6
∴ r = 3 cm.
0
Updated: 15 hours ago
৩৪ সে.মি. ব্যাস বিশিষ্ট বৃত্তের কেন্দ্র হতে ৮ সে.মি. দূরত্বে অবস্থিত জ্যা এর দৈর্ঘ্য কত?
Created: 1 month ago
A
২০ সে.মি.
B
২৬ সে.মি.
C
২৮ সে.মি.
D
৩০ সে.মি.
গণিত
ঘন জ্যামিতি (Solid geometry)
জ্যামিতি (geometry)
জ্যামিতি প্রাথমিক ধারণা (Basic Concept)
ত্রিভুজ (Triangle)
বৃত্ত (Circle)
সমাধান:
দেওয়া আছে, কেন্দ্র হতে জ্যা এর দূরত্ব OC = ৮ সে.মি.
ব্যাস = ৩৪ সে.মি.
ব্যাসার্ধ OB = ৩৪/২ = ১৭ সে.মি.
AB জ্যা এর অর্ধাংশ = BC
কেন্দ্র হতে জ্যা এর দূরত্ব = OC
∴ পিথাগোরাসের উপপাদ্য অনুসারে,
OB২ = OC২ + BC২
⇒ BC২ = OB২ - OC২
⇒ BC = √(OB২ - OC২)
⇒ BC = √{(১৭)২ - (৮)২}
⇒ BC = √(২৮৯- ৬৪)
⇒ BC = √২২৫
⇒ BC = ১৫
∴ জ্যা AB এর দৈর্ঘ্য = BC × ২ = ১৫ × ২ = ৩০ সে.মি
0
Updated: 1 month ago