Question: If C is the midpoint of the points A(2, - 1) and B(8, 5), find the length of AC.

Solution:
দেওয়া আছে,
 A(2, - 1) এবং B(8, 5), 
এবং C হলো AB-এর মধ্যবিন্দু।

দূরত্বের সূত্র ব্যবহার করে AB-এর দৈর্ঘ্য নির্ণয় করি,
AB = √(x2 - x1)2 + (y2 - y1)2)
= √(8 - 2)2 + {5 - (-1)}2
= √(62 + 62)
= √(36 + 36)
= √72
= √(36 × 2)
= 6√2

C হলো AB এর মধ্যবিন্দু, তাই AC = AB/2
 = 6√2/2
 = 3√2

প্রশ্ন: একটি সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য লম্ব অপেক্ষা 1 মিটার কম এবং লম্ব অপেক্ষা অতিভুজের দৈর্ঘ্য 1 মিটার বেশি হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত? 

সমাধান: 
ধরি, 
সমকোণী ত্রিভুজের লম্বের দৈর্ঘ্য = x
∴ সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য = x - 1
∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = x + 1 

আমরা জানি,
(অতিভুজ)2 = (লম্ব)2 + (ভূমি)2 
⇒ (x + 1)2 = (x - 1)2 + x2 
⇒ x2 + 2x + 1 = x2 - 2x + 1 + x2 
⇒ x2 - 4x = 0 
⇒ x(x - 4) = 0 
⇒ x = 4  [যেহেতু, ত্রিভুজের লম্ব কখনো শূন্য হতে পারে না]

∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = (x + 1) মিটার 
= (4 + 1) মিটার 
= 5 মিটার ।

Question: In the figure, AOB is a straight line. What is the average of the four numbers a, b, c, and d?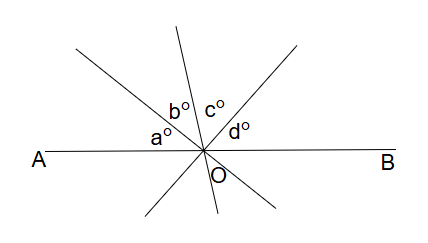

Solution:
যেহেতু, AOB একটি সরলরেখা, তাই সরলরেখার উপর উৎপন্ন কোণগুলোর সমষ্টি ১৮০°।
∴ a° + b° + c° + d° = 180°
⇒ a + b + c + d = 180
এখন, চারটি সংখ্যার গড় = (সংখ্যাগুলোর সমষ্টি) ÷ (মোট সংখ্যা)
= (a + b + c + d) ÷ 4
= 180 ÷ 4
= 45
∴ a, b, c এবং d চারটি সংখ্যার গড় হলো 45।