প্রশ্ন: একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের পার্থক্য 6 ডিগ্রি হলে, ক্ষুদ্রতম কোণের মান কত? 

সমাধান: 
ধরি, 
ক্ষুদ্রতম কোণ = x
এবং অপর ক্ষুদ্রতম কোণ = x + 6° 

এখন, 
x + x + 6° + 90° = 180° 
⇒ 2x + 96° = 180°
⇒ 2x = 180° - 96°
⇒ x = 84°/2
∴ x = 42°

∴ ক্ষুদ্রতম কোণ = 42° ।

প্রশ্ন: কোনো একটি ত্রিভুজের দুইটি কোণের পরিমাণ ৩৪° ও ৫৬°। ত্রিভুজটি কোন ধরনের?

সমাধান:
আমরা জানি,
ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণ বা ১৮০°

ধরি,
৩য় কোণটি ‘ক’

প্রশ্নমতে,
⇒ ৩৪° + ৫৬° + ক = ১৮০°
⇒ ৯০° + ক = ১৮০°
⇒ ক = ১৮০° - ৯০°
∴ ক = ৯০°

অর্থাৎ তৃতীয় কোণ ৯০°, যা একটি সমকোণ।
সুতরাং, ত্রিভুজটি একটি সমকোণী ত্রিভুজ।

প্রশ্ন: ΔABC ত্রিভুজের ∠B এর পরিমাণ ৫২° এবং AB = AC হয়, তাহলে ∠A এর মান কত?

সমাধান:

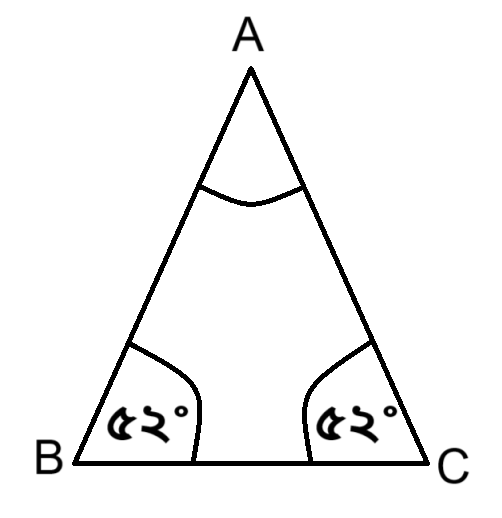
চিত্রে, ∠B = ৫২° এবং AB = AC 
∴ ∠B = ∠C = ৫২°
আমরা জানি,
ত্রিভুজের তিনটি কোণের সমষ্টি ১৮০°

প্রশ্নমতে,
⇒ ∠A + ∠B + ∠C = ১৮০°
⇒ ∠A + ৫২° + ৫২° = ১৮০°
⇒ ∠A + ১০৪° = ১৮০°
⇒ ∠A = ১৮০° - ১০৪° = ৭৬°
∴ ∠A = ৭৬°