কোন পরীক্ষায় ৭৫% গণিতে এবং ৬৫% বাংলায় পাশ করল। উভয় বিষয়ে পাশ করল ৫৫%। উভয় বিষয়ে শতকরা কতজন ফেল করল?
A
১০%
B
১৫%
C
২০%
D
২৫%
উত্তরের বিবরণ
প্রশ্ন: কোন পরীক্ষায় ৭৫% গণিতে এবং ৬৫% বাংলায় পাশ করল। উভয় বিষয়ে পাশ করল ৫৫%। উভয় বিষয়ে শতকরা কতজন ফেল করল?
সমাধান:
গণিতে পাশ = n(M) = ৭৫%
বাংলায় পাশ = n(B) = ৬৫%
উভয় বিষয়ে পাশ = n(M ∩ B) = ৫৫%
যে কোনো এক বিষয় বা উভয় বিষয়ে পাশ = n(M ∪ B)
n(M ∪ B) = n(M) + n(B) - n(M ∩ B)
= ৭৫% + ৬৫% - ৫৫%
= ১৪০% - ৫৫%
= ৮৫%
∴ উভয় বিষয়ে ফেল করল = ১০০% - ৮৫%
= ১৫%
0
Updated: 15 hours ago
৬ জন লোক ও
৮ জন মহিলা ১টি
কাজ ১০ দিনে শেষ
করতে পারে। একই কাজ ১৩
জন লোক ও ২৪
জন মহিলা ৪ দিনে শেষ
করতে পারে। ১০ জন লোক
ও ৫ জন মহিলা
ঐ কাজ কত দিনে
করতে পারবে?
Created: 3 weeks ago
A
৬ দিন
B
৮ দিন
C
১০ দিন
D
১২ দিন
প্রশ্ন: ৬ জন লোক ও ৮ জন মহিলা ১টি কাজ ১০ দিনে শেষ করতে পারে। একই কাজ ১৩ জন লোক ও ২৪ জন মহিলা ৪ দিনে শেষ করতে পারে। ১০ জন লোক ও ৫ জন মহিলা ঐ কাজ কত দিনে করতে পারবে?
সমাধান:
ধরি,
লোক = ক এবং মহিলা = খ
প্রশ্নমতে,
(৬ক + ৮খ) × ১০ = (১৩ক + ২৪খ) × ৪
⇒ ৬০ক + ৮০খ = ৫২ক + ৯৬খ
⇒ ৬০ক - ৫২ক = ৯৬খ - ৮০খ
⇒ ৮ক = ১৬খ
⇒ ক = ২খ
অর্থাৎ, ১ জন লোক দুইজন মহিলার সমান কাজ করতে পারে।
তাহলে,
{(৬ × ২) + ৮} বা ২০ জন মহিলা ১টি কাজ করে = ১০ দিনে
∴ ১ জন মহিলা কাজটি করবে = (২০ × ১০) দিনে
∴ {(১০ × ২) + ৫} বা ২৫ জন মহিলা ঐ কাজটি করবে = (২০ × ১০)/২৫ দিনে
= ৮ দিনে
0
Updated: 3 weeks ago
এর সমাধান-
Created: 4 weeks ago
A
2/5
B
1
C
11/13
D
7/2
গণিত
অসমতা (Inequality)
বীজগণিত (Algebra)
সরল সমীকরণ (Simple/linear equation)
সরলীকরণ (Simplification)
প্রশ্ন: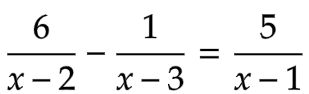 
এর সমাধান-
সমাধান: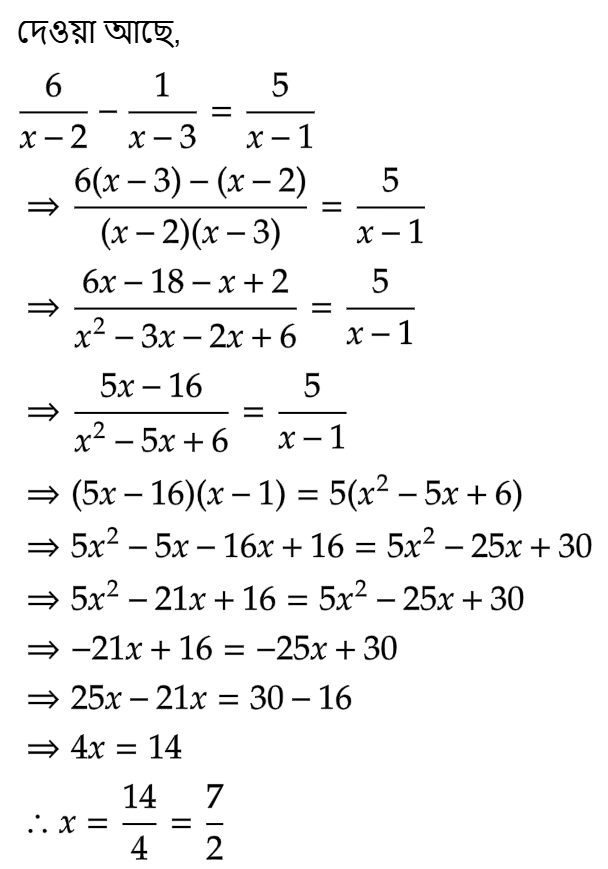
0
Updated: 4 weeks ago
(2x - 1)(x + 3) = 2x(x + 1) হলে, x এর মান কত?
Created: 3 weeks ago
A
0
B
1
C
- 2
D
2
প্রশ্ন: (2x - 1)(x + 3) = 2x(x + 1) হলে, x এর মান কত?
সমাধান:
দেওয়া আছে,
(2x - 1)(x + 3) = 2x(x + 1)
⇒ 2x2 + 6x - x - 3 = 2x2 + 2x
⇒ 2x2 + 5x - 3 = 2x2 + 2x
⇒ 2x2 + 5x - 3 - 2x2 - 2x = 0
⇒ 3x - 3 = 0
⇒ 3(x - 1) = 0
⇒ x - 1 = 0
∴ x = 1
0
Updated: 3 weeks ago
