ΔPQR সমবাহু ত্রিভুজের একটি মধ্যমা PM এবং G ভরকেন্দ্র। GM = 6 সেমি হলে PM = ?
A
12 সেমি
B
15 সেমি
C
18 সেমি
D
22 সেমি
উত্তরের বিবরণ

আমরা জানি,
ত্রিভুজের ভরকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে বিভক্ত করে।
এখানে, মধ্যমা PM এবং ভরকেন্দ্র G।
সুতরাং, PG : GM = 2 : 1
দেওয়া আছে, GM = 6 সেমি।
প্রশ্নমতে,
PG/GM = 2/1
বা, PG/6 = 2
বা, PG = 6 × 2
∴ PG = 12 সেমি
এখন, মধ্যমা PM এর মোট দৈর্ঘ্য হলো এর দুটি অংশের যোগফল।
PM = PG + GM
= 12 + 6
= 18 সেমি
অতএব, PM এর দৈর্ঘ্য 18 সেমি।
ত্রিভুজের ভরকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে বিভক্ত করে।
এখানে, মধ্যমা PM এবং ভরকেন্দ্র G।
সুতরাং, PG : GM = 2 : 1
দেওয়া আছে, GM = 6 সেমি।
প্রশ্নমতে,
PG/GM = 2/1
বা, PG/6 = 2
বা, PG = 6 × 2
∴ PG = 12 সেমি
এখন, মধ্যমা PM এর মোট দৈর্ঘ্য হলো এর দুটি অংশের যোগফল।
PM = PG + GM
= 12 + 6
= 18 সেমি
অতএব, PM এর দৈর্ঘ্য 18 সেমি।
0
Updated: 1 month ago
x + y - 1 = 0, x - y + 1 = 0 এবং y + 3 = 0 সরল রেখা তিনটি দ্বারা গঠিত ত্রিভুজটি-
Created: 5 months ago
A
সমবাহু
B
বিষমবাহু
C
সমকোণী
D
সমদ্বিবাহু
প্রশ্ন: x + y - 1 = 0, x - y + 1 = 0 এবং y + 3 = 0 সরল রেখা তিনটি দ্বারা গঠিত ত্রিভুজটি-
সমাধান:
x + y - 1 = 0
⇒ y = - x + 1
∴ সমীকরণটির ঢাল = -1
আবার,
x - y + 1 = 0
⇒ y = x + 1
∴ সমীকরণটির ঢাল = 1
এখন,
ঢালদ্বয়ের গুণফল = -1, তাই সমীকরণদ্বয় পরস্পর লম্ব।
∴ ত্রিভুজটি সমকোণী।
0
Updated: 5 months ago
কোন তিনটি বাহু দ্বারা ত্রিভুজ আঁকা সম্ভব নয়?
Created: 1 month ago
A
২, ৫ এবং ৬
B
৩, ৪ এবং ৫
C
২, ৩ এবং ৫
D
৫, ৬ এবং ৮
প্রশ্ন: কোন তিনটি বাহু দ্বারা ত্রিভুজ আঁকা সম্ভব নয়?
সমাধান:
আমরা জানি,
ত্রিভুজের যেকোনো দুই বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বৃহত্তম।
এখানে,
প্রত্যেকটি ত্রিভুজের ক্ষুদ্রতম দুইটি বাহুর যোগফলকে তৃতীয় (বৃহত্তম) বাহুর সাথে তুলনা করে পাই,
৩ + ৪ = ৭ > ৫ ; ত্রিভুজ আঁকা সম্ভব,
২ + ৫ = ৭ > ৬ ; ত্রিভুজ আঁকা সম্ভব,
২ + ৩ = ৫ = ৫ ; ত্রিভুজ আঁকা সম্ভব নয় এবং
৫ + ৬ = ১১ > ৮ ; ত্রিভুজ আঁকা সম্ভব।
0
Updated: 1 month ago
নিচের চিত্রে মোট কয়টি ত্রিভুজ আছে?
Created: 3 months ago
A
৪টি
B
৫টি
C
৬টি
D
৭টি
প্রশ্ন: নিচের চিত্রে মোট কয়টি ত্রিভুজ আছে?
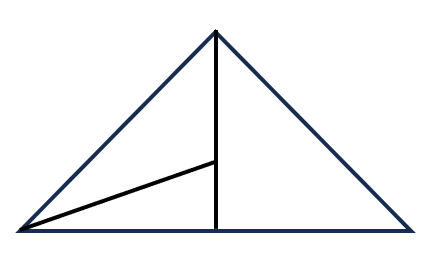
সমাধান:
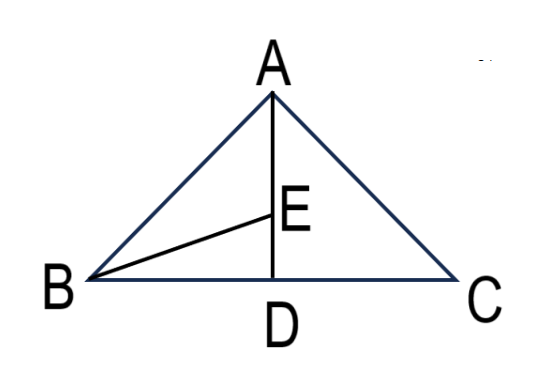
এখানে,
১টি ফাঁকা স্থান নিয়ে ত্রিভুজ আছে, ABE, BDE, ACD = ৩টি
২টি ফাঁকা স্থান নিয়ে ত্রিভুজ আছে, ABD = ১টি
৩টি ফাঁকা স্থান নিয়ে ত্রিভুজ আছে, ABC = ১টি
∴ মোট ত্রিভুজ আছে = ৩ + ১ + ১ = ৫টি
---------------------------------------
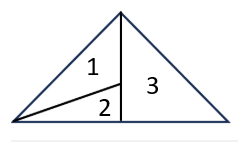
ত্রিভুজগুলো হলো: 1, 2, 3, 12, 123
∴ মোট ত্রিভুজ আছে = ৫টি
0
Updated: 3 months ago