একটি সুষম বহুভুজের প্রতিটি অন্তঃকোণ ও বহিঃকোণের পার্থক্য 132° হলে বহুভুজটি কোন প্রকৃতির?
A
অষ্টভুজ
B
দশভুজ
C
পঞ্চদশভুজ
D
ষোড়শভুজ
উত্তরের বিবরণ
সমাধান:
মনে করি, বহুভুজের বাহু সংখ্যা = n
আমরা জানি:
প্রতিটি অন্তঃকোণ = (n - 2) × 180°/n
প্রতিটি বহিঃকোণ = 360°/n
প্রশ্নমতে,
অন্তঃকোণ - বহিঃকোণ = 132°
বা, {(n - 2) × 180°/n} - (360°/n) = 132°
বা, {(n - 2) × 180° - 360°}/n = 132°
বা, 180°n - 360° - 360° = 132°n
বা, 180°n - 720° = 132°n
বা, 180°n - 132°n = 720°
বা, 48°n = 720°
বা, n = 720°/48°
বা, n = 15
যেহেতু বহুভুজটির বাহু সংখ্যা 15, এটি একটি পঞ্চদশভুজ (Pentadecagon)।
মনে করি, বহুভুজের বাহু সংখ্যা = n
আমরা জানি:
প্রতিটি অন্তঃকোণ = (n - 2) × 180°/n
প্রতিটি বহিঃকোণ = 360°/n
প্রশ্নমতে,
অন্তঃকোণ - বহিঃকোণ = 132°
বা, {(n - 2) × 180°/n} - (360°/n) = 132°
বা, {(n - 2) × 180° - 360°}/n = 132°
বা, 180°n - 360° - 360° = 132°n
বা, 180°n - 720° = 132°n
বা, 180°n - 132°n = 720°
বা, 48°n = 720°
বা, n = 720°/48°
বা, n = 15
যেহেতু বহুভুজটির বাহু সংখ্যা 15, এটি একটি পঞ্চদশভুজ (Pentadecagon)।
0
Updated: 1 month ago
সূর্যের উন্নতি কোণ 60° হলে একটি মিনারের ছায়ার দৈর্ঘ্য 240 মিটার হয়। মিনারটির উচ্চতা কত?
Created: 1 month ago
A
418.45 মি.
B
319.69 মি.
C
415.69 মি.
D
315.69 মি.
প্রশ্ন: সূর্যের উন্নতি কোণ 60° হলে একটি মিনারের ছায়ার দৈর্ঘ্য 240 মিটার হয়। মিনারটির উচ্চতা কত?
সমাধান:
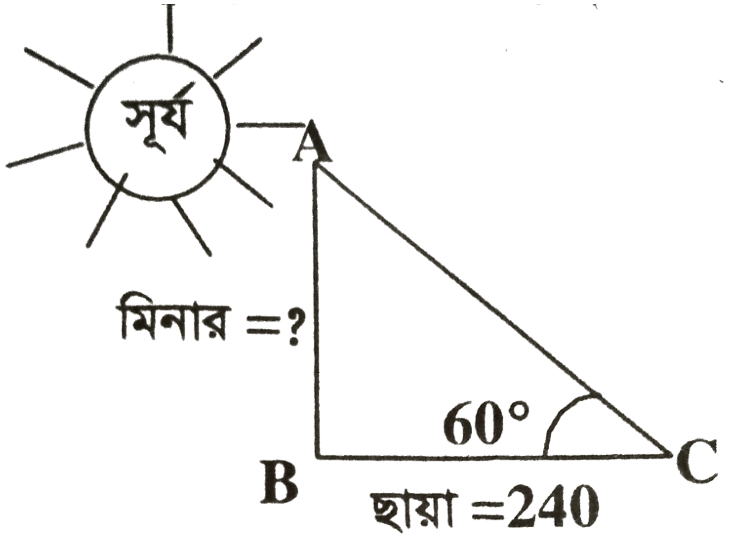
দেওয়া আছে,
মিনারের ছায়ার দৈর্ঘ্য, BC = 240 মিটার
সূর্যের উন্নতি কোণ, θ = 60°
মিনারটির উচ্চতা, AB (h) =?
চিত্র হতে পাই,
tanθ = AB/BC
বা, tan60° = AB/240
বা, √3 = AB/240
বা, AB = 240 × √3
∴ AB = 415.69 মিটার
∴ মিনারটির উচ্চতা = 415.69 মিটার।
0
Updated: 1 month ago
একটি বেলনের বক্রতলের ক্ষেত্রফল 25 বর্গমিটার ও আয়তন 100 ঘনমিটার। বেলনটির ভূমির ব্যাসার্ধ কত?
Created: 1 month ago
A
8 মিটার
B
6 মিটার
C
4 মিটার
D
12 মিটার
প্রশ্ন: একটি বেলনের বক্রতলের ক্ষেত্রফল 25 বর্গমিটার ও আয়তন 100 ঘনমিটার। বেলনটির ভূমির ব্যাসার্ধ কত?
সমাধান:
আমরা জানি,
বেলনের বক্রতলের ক্ষেত্রফল = 2πrh বর্গ একক ও
বেলনের বক্রতলের আয়তন = πr2h ঘন একক
দেওয়া আছে,
বেলনের বক্রতলের ক্ষেত্রফল, 2πrh = 25
ও বেলনের বক্রতলের আয়তন, πr2h =100
প্রশ্নমতে,
(2πrh)/(πr2h) = 25/100
বা, 2/r = 1/4
∴ r = 8
∴ বেলনের ভূমির ব্যাসার্ধ = 8 মিটার।
0
Updated: 1 month ago
একটি সংখ্যা ১০% বৃদ্ধি পাওয়ার পর পুনরায় ২০% বৃদ্ধি পেয়ে ৬৬০ হলে প্রাথমিক সংখ্যাটি কত?
Created: 1 month ago
A
৪০০
B
৪৮০
C
৫০০
D
৫৫০
সমাধান:
ধরি,
প্রাথমিক সংখ্যাটি = ক
এখন,
১০% বৃদ্ধি পাওয়ায় সংখ্যাটি হয়,
= ক + ক এর ১০%
= ক + (১০ক/১০০)
= ক + (ক/১০)
= ১১ক/১০
প্রশ্নমতে,
(১১ক/১০) + (১১ক/১০) এর ২০% = ৬৬০
⇒ (১১ক/১০) + (১১ক/১০) × (২০/১০০) = ৬৬০
⇒ (১১ক/১০) + (১১ক/৫০) = ৬৬০
⇒ (৫৫ক + ১১ক)/৫০ = ৬৬০
⇒ ৬৬ক = ৬৬০ × ৫০
⇒ ক = (৬৬০ × ৫০)/৬৬
⇒ ক = ৫০০
শর্টকাট:
সংখ্যাটি = ৬৬০ × {১০০/(১০০ + ১০)}{১০০/(১০০ + ২০)}
= ৬৬০ × (১০০/১১০) × (১০০/১২০)
= ৬ × (১০০) × (৫/৬)
= ৫০০
0
Updated: 1 month ago