একটি মইয়ের এক প্রান্ত ভূমি থেকে 12 মিটার উঁচু ঘরের শীর্ষবিন্দু বরাবর পৌঁছায় এবং অপর প্রান্ত ঘর থেকে 5 মিটার দূরে থাকে। মইটির দৈর্ঘ্য কত?
A
11 মিটার
B
13 মিটার
C
15 মিটার
D
17 মিটার
উত্তরের বিবরণ

মনে করি,
ঘরের শীর্ষবিন্দুর অবস্থান = A,
ঘরের উচ্চতা AB = 12 মিটার,
ঘর থেকে মইয়ের নিচের প্রান্তের দূরত্ব BC = 5 মিটার,
মইটির দৈর্ঘ্য = AC
ABC সমকোণী ত্রিভুজে,
পিথাগোরাসের উপপাদ্য অনুযায়ী,
AC2 = AB2 + BC2
⇒ AC2 = 122 + 52
⇒ AC2 = 144 + 25
⇒ AC2 = 169
⇒ AC = √169
⇒ AC = 13
∴ মইটির দৈর্ঘ্য = 13 মিটার
ঘরের শীর্ষবিন্দুর অবস্থান = A,
ঘরের উচ্চতা AB = 12 মিটার,
ঘর থেকে মইয়ের নিচের প্রান্তের দূরত্ব BC = 5 মিটার,
মইটির দৈর্ঘ্য = AC
ABC সমকোণী ত্রিভুজে,
পিথাগোরাসের উপপাদ্য অনুযায়ী,
AC2 = AB2 + BC2
⇒ AC2 = 122 + 52
⇒ AC2 = 144 + 25
⇒ AC2 = 169
⇒ AC = √169
⇒ AC = 13
∴ মইটির দৈর্ঘ্য = 13 মিটার
0
Updated: 1 month ago
If y = sin(sinx) then what is the value of dy/dx?
Created: 1 month ago
A
cos(sinx)
B
cosx.cos(cosx)
C
cos2x
D
cosx.cos(sinx)
Question: If y = sin(sinx) then what is the value of dy/dx?
Solution: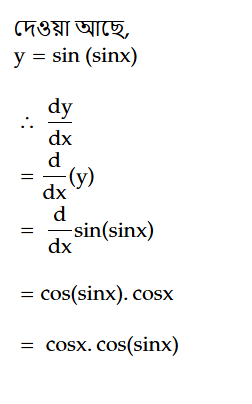
0
Updated: 1 month ago
cosec(90° - θ) = 3 হলে, cosθ = কত?
Created: 2 months ago
A
3
B
√3
C
1/3
D
1/√3
সমাধান:
cosec(90° - θ) = 3
বা, secθ = 3
বা, 1/cosθ = 3
∴ cosθ = 1/3
0
Updated: 2 months ago
একটি খুঁটির দৈর্ঘ্য 60√3 মিটার। এর ছায়ার দৈর্ঘ্য কত মিটার হলে সূর্যের উন্নতি কোণ 60° হবে?
Created: 3 months ago
A
20√3 মিটার
B
30 মিটার
C
40√3 মিটার
D
60 মিটার
0
Updated: 3 months ago