একটি 48 মিটার লম্বা খুঁটি ভেঙে গিয়ে সম্পূর্ণভাবে বিচ্ছিন্ন না হয়ে ভূমির সাথে 30° কোণ উৎপন্ন করে। খুঁটিটি কত উঁচুতে ভেঙ্গে ছিল?
A
14 মিটার
B
16 মিটার
C
18 মিটার
D
20 মিটার
উত্তরের বিবরণ
প্রশ্ন: একটি 48 মিটার লম্বা খুঁটি ভেঙে গিয়ে সম্পূর্ণভাবে বিচ্ছিন্ন না হয়ে ভূমির সাথে 30° কোণ উৎপন্ন করে। খুঁটিটি কত উঁচুতে ভেঙ্গে ছিল?
সমাধান:
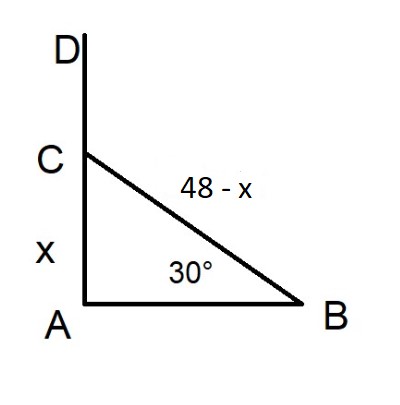
ধরি,
খুটিটি x মিটার উচুতে ভেঙ্গেছিল।
∴ অপর ভাঙ্গা অংশের দৈর্ঘ্য = (48 - x) মিটার
sinθ = x/(48 - x)
sin30° = x/(48 - x)
বা, 1/2 = x/(48 - x)
2x = 48 - x
2x + x = 48
3x = 48
∴ x = 16
0
Updated: 3 months ago
একটি আয়তাকার ঘরের দৈর্ঘ্য বিস্তারের দ্বিগুণ। এর ক্ষেত্রফল 512 বর্গমিটার হলে, পরিসীমা কত?
Created: 3 months ago
A
98 মিটার
B
96 মিটার
C
94 মিটার
D
92 মিটার
প্রশ্ন: একটি আয়তাকার ঘরের দৈর্ঘ্য বিস্তারের দ্বিগুণ। এর ক্ষেত্রফল 512 বর্গমিটার হলে, পরিসীমা কত?
সমাধান:
ধরি,
আয়তাকার ঘরের বিস্তার = x মিটার
∴ আয়তাকার ঘরের দৈর্ঘ্য = 2x মিটার
প্রশ্নমতে,
2x × x = 512
⇒ x2 = 512/2
⇒ x2 = 256
∴ x = 16
দৈর্ঘ্য = (16 × 2) মিটার
= 32 মিটার
আয়তাকার ঘরের পরিসীমা = 2(32 + 16) মিটার
= 2 × 48 মিটার
= 96 মিটার
0
Updated: 3 months ago
পাঁচ অঙ্কের ক্ষুদ্রতম সংখ্যা ও চার অঙ্কের বৃহত্তম সংখ্যার অন্তর কত?
Created: 3 months ago
A
৯
B
১০
C
১
D
- ১
প্রশ্ন: পাঁচ অঙ্কের ক্ষুদ্রতম সংখ্যা ও চার অঙ্কের বৃহত্তম সংখ্যার অন্তর কত?
সমাধান:
পাঁচ অঙ্কের ক্ষুদ্রতম সংখ্যা = ১০০০০
চার অঙ্কের বৃহত্তম সংখ্যা = ৯৯৯৯
∴ অন্তর = ১০০০০ - ৯৯৯৯ = ১
0
Updated: 3 months ago
৩৫০ টাকা দরে ৩ কেজি মিষ্টি কিনে ৪ টাকা হারে ভ্যাট দিলে মোট কত ভ্যাট দিতে হবে?
Created: 2 months ago
A
১৪ টাকা
B
৪২ টাকা
C
১২ টাকা
D
১০৫ টাকা
প্রশ্ন: ৩৫০ টাকা দরে ৩ কেজি মিষ্টি কিনে ৪ টাকা হারে ভ্যাট দিলে মোট কত ভ্যাট দিতে হবে?
সমাধান:
১ কেজি মিষ্টির দাম = ৩৫০ টাকা
∴ ৩ কেজি মিষ্টির দাম = (৩৫০ × ৩) টাকা
= ১০৫০ টাকা
১০০ টাকায় ভ্যাট ৪ টাকা
∴ ১০৫০ টাকায় ভ্যাট = (৪ × ১০৫০)/১০০ টাকা
= ৪২ টাকা
0
Updated: 2 months ago