1 + 2 + 3 + 4 +.................+ 99 = কত?
A
4650
B
4750
C
4850
D
4950
উত্তরের বিবরণ
প্রশ্ন: 1 + 2 + 3 + 4 + ……………. + 99 = কত?
সমাধান:
n সংখ্যক স্বাভাবিক সংখ্যার সমষ্টি = n(n + 1)/2
∴ 99 স্বাভাবিক সংখ্যার সমষ্টি = 99(99 + 1)/2
= (100 × 99)/2
= 50 × 99
= 4950
0
Updated: 3 months ago
x+ 1/x= √3 হলে x 3 + 1/x 3 = ?
Created: 6 months ago
A
6
B
4
C
0
D
2
0
Updated: 6 months ago
If HOUSE = 81521195 and TREE = 201855, then GARDEN will be equal to-
Created: 1 month ago
A
71518414
B
7184514
C
71845141
D
71184514
Question: If HOUSE = 81521195 and TREE = 201855, then GARDEN will be equal to-
Solution: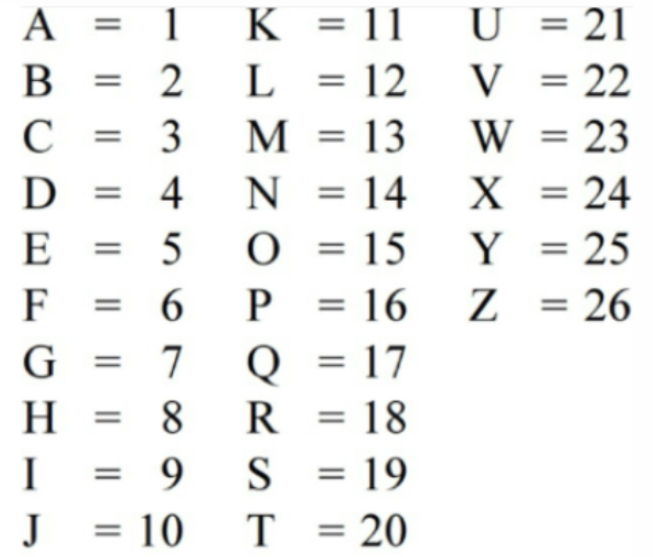
According to the English alphabet,
HOUSE = 8 15 21 19 5
And,
TREE = 20 18 5 5
Now,
GARDEN = 7 1 18 4 5 14
So the code is- 71184514
∴ GARDEN = 71184514
0
Updated: 1 month ago
x2 - 3x + 1 = 0 হলে (x2 - 1/x2) এর মান -
Created: 2 months ago
A
5√3
B
3√5
C
4√5
D
6√5
প্রশ্ন: x2 - 3x + 1 = 0 হলে (x2 - 1/x2) এর মান-
সমাধান:
x2 - 3x + 1 = 0
⇒ x2 + 1 = 3x
⇒ (x2 + 1)/x = (3x)/x
∴ x + 1/x = 3
আমরা জানি,
(x - 1/x)2 = (x + 1/x)2 - 4.x.(1/x)
⇒ (x - 1/x)2 = (3)2 - 4
⇒ (x - 1/x)2 = 9 - 4
⇒ (x - 1/x)2 = 5
∴ x - 1/x = √5
x2 - 1/x2 = (x)2 - (1/x)2
= (x + 1/x)(x - 1/x)
= 3√5
0
Updated: 2 months ago