৩ দিনে একটি কাজের ১/২৭ অংশ শেষ হলে ঐ কাজের ৩ গুণ কাজ করতে কত দিন লাগবে?
A
৮১ দিন
B
৯ দিন
C
২৪৩ দিন
D
২৭ দিন
উত্তরের বিবরণ
প্রশ্ন: ৩ দিনে একটি কাজের ১/২৭ অংশ শেষ হলে ঐ কাজের ৩ গুণ কাজ করতে কত দিন লাগবে?
সমাধান:
১/২৭ অংশ কাজ করে ৩ দিনে
∴ ১ বা সম্পূর্ণ অংশ কাজ করে = (২৭ × ৩) দিনে
= ৮১ দিনে।
সুতরাং, তিন গুণ কাজ করে = (৮১ × ৩) দিনে
= ২৪৩ দিনে
0
Updated: 3 months ago
তিনটি নিরপেক্ষ মুদ্রা একত্রে নিক্ষেপ করা হলে দুইটি হেড ও একটি টেল পাওয়ার সম্ভাবনা কত?
Created: 1 month ago
A
1/8
B
1/2
C
1/4
D
3/8
সমাধান:
তিনটি নিরপেক্ষ মুদ্রা একবার নিক্ষেপ করলে মোট নমুনা বিন্দু হবে = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} = 8 টি
দুইটি হেড ও একটি টেল পাওয়ার অনুকূল ঘটনাগুলো = {HHT, HTH, THH} = 3 টি।
∴ দুইটি হেড ও একটি টেল পাওয়ার সম্ভাবনা = 3/8
0
Updated: 1 month ago
একটি ব্যাংকে নির্দিষ্ট পরিমাণ টাকা জমা রাখলে জমাকৃত টাকা সরল মুনাফায় ২ বছরে ৫/৪ অংশ হয়। ব্যাংকের মুনাফার হার কত?
Created: 1 month ago
A
৮%
B
১০%
C
১২.৫%
D
১৪%
প্রশ্ন: একটি ব্যাংকে নির্দিষ্ট পরিমাণ টাকা জমা রাখলে জমাকৃত টাকা সরল মুনাফায় ২ বছরে ৫/৪ অংশ হয়। ব্যাংকের মুনাফার হার কত?
সমাধান:
ধরি,
মূলধন = P
মুনাফা = I
আমরা জানি,
মুনাফা-আসল = I + P
⇒ মূলধনের ৫/৪ অংশ = I + P
⇒ P × (৫/৪) = I + P
⇒ I = (৫P/৪) - P
⇒ I = (৫P - ৪P)/৪
⇒ I = P/৪
∴ মুনাফা, I = Pnr/১০০
⇒ P/৪ = (P × ২ × r)/১০০
⇒ r = (১০০ × P)/(P × ২ × ৪)
⇒ r = ১০০/৮ = ১২.৫
অর্থাৎ মুনাফার হার = ১২.৫ %
0
Updated: 1 month ago
একটি মিনারের পাদদেশ হতে ২০ মিটার দূরের একটি স্থান হতে মিনারটির শীর্ষবিন্দুর উন্নতি কোণ 30° হলে মিনারটির উচ্চতা কত?
Created: 2 months ago
A
20√7 মিটার
B
20/√3 মিটার
C
20 মিটার
D
10√3 মিটার
প্রশ্ন: একটি মিনারের পাদদেশ হতে ২০ মিটার দূরের একটি স্থান হতে মিনারটির শীর্ষবিন্দুর উন্নতি কোণ 30° হলে মিনারটির উচ্চতা কত?
সমাধান:
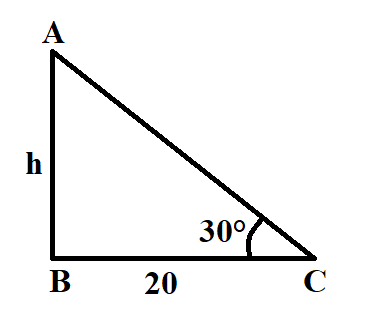
ধরি,
মিনারটির উচ্চতা, AB = h
মিনারের পাদদেশ হতে BC = ২০ মিটার দূরের একটি স্থান হতে মিনারটির শীর্ষ বিন্দুর উন্নতি কোণ ∠ACB = ৩০°
আমরা জানি,
tan∠ACB = AB/BC
বা, tan30° = h/20
বা, 1/√3 = h/20
∴ h = 20/√3
∴ মিনারটির উচ্চতা = 20/√3
0
Updated: 2 months ago