যদি sinθ = √2 - cosθ হয়, তবে θ এর মান কত? যেখানে, 0 < θ < π/2.
A
π/2
B
π/4
C
π/3
D
2π
উত্তরের বিবরণ
সমাধান:
sinθ = √2 - cosθ
⇒ sinθ = √2 - cosθ
⇒ sin2θ = (√2 - cosθ)2
⇒ 1 - cos2θ = (√2)2 - 2.√2.cosθ + cos2θ
⇒ 1 - cos2θ = 2 - 2√2cosθ + cos2θ
⇒ 2cos2θ - 2√2cosθ + 1 = 0
⇒ (√2cosθ - 1)2 = 0
⇒ √2cosθ - 1 = 0
⇒ √2cosθ = 1
⇒ cosθ = 1/√2
⇒ cosθ = cos45°
⇒ cosθ = cos(π/4)
∴ θ = π/4
0
Updated: 1 month ago
A = 45° হলে, cosA.sin2A এর মান কত?
Created: 2 months ago
A
1
B
1/2
C
1/√2
D
- 1/√2
সমাধান:
দেওয়া আছে,
A = 45°
আমরা জানি,
cos2A.sinA = cos45°sin90°
= (1/√2) × 1
= 1/√2
0
Updated: 2 months ago
কোনো বৃত্তের কেন্দ্রস্থ কোণ ৭২° হলে, বৃত্তস্থ কোণ কত হবে?
Created: 2 months ago
A
৪২°
B
১৪৪°
C
৩৬°
D
১২০°
সমাধান:
জ্যামিতির সূত্র অনুযায়ী, একই চাপের উপর দাঁড়ানো বৃত্তস্থ কোণ হলো কেন্দ্রস্থ কোণের অর্ধেক।
অতএব,
উত্তর: ৩৬° ✅
0
Updated: 2 months ago
সমাধান করুন:
Created: 2 months ago
A
3tanθ
B
cotθ
C
2secθ
D
কোনটিই নয়
প্রশ্ন:
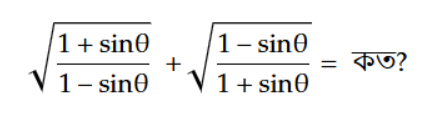
সমাধান:
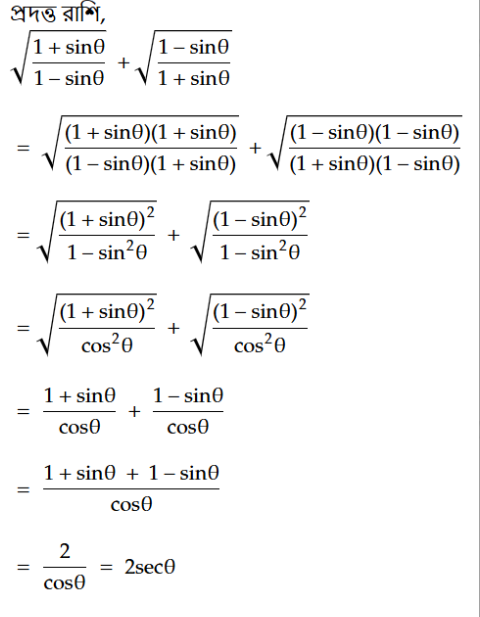
0
Updated: 2 months ago