প্রশ্নবোধক চিহ্নিত ঘরে কোন সংখ্যাটি বসবে?
A
৪
B
৫
C
৬
D
৭
উত্তরের বিবরণ
প্রশ্ন: প্রশ্নবোধক চিহ্নিত ঘরে কোন সংখ্যাটি বসবে?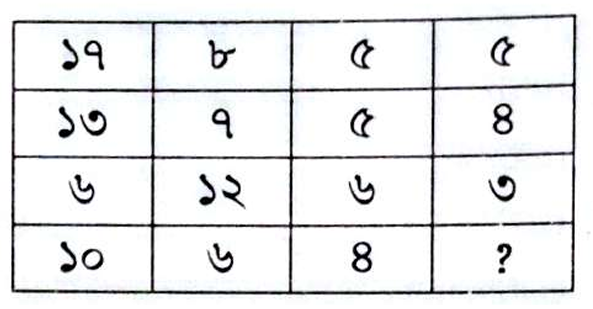
সমাধান:
১৭ + ৮ = ২৫ ; ৫ × ৫ = ২৫
১৩ + ৭ = ২০ ; ৫ × ৪ = ২০
৬ + ১২ = ১৮ ; ৬ × ৩ = ১৮
১০ + ৬ = ১৬ ; ৪ × ৪ = ১৬
সুতরাং, প্রশ্নবোধক চিহ্নিত ঘরে ৪ বসবে।
0
Updated: 22 hours ago
Created: 2 weeks ago
A
B
C
D
প্রশ্ন:
সমাধান:
1
1 + 2 = 3
3 + 2 = 5
5 + 2 = 7
A এর ১ বর্ণ পর C
C এর ১ বর্ণ পর E
E এর ১ বর্ণ পর G
∴ সঠিক উত্তর 7/G.
0
Updated: 2 weeks ago
প্রশ্নবােধক চিহ্নিত স্থানে কোন সংখ্যা বসবে?
Created: 2 weeks ago
A
১৮
B
৬৮
C
৮১
D
৮৮
প্রশ্ন: প্রশ্নবােধক চিহ্নিত স্থানে কোন সংখ্যা বসবে?
সমাধান:
১ম চিত্রে,
৮ × ৪ + ৭ = ৩৯
২য় চিত্র,
৩ × ৬ + ৯ = ২৭
৩য় চিত্রে,
৭ × ৯ + ৫ = ৬৮
0
Updated: 2 weeks ago
কোন শব্দযুগলটি ভিন্ন?
Created: 3 weeks ago
A
False, True
B
Sharp, Blunt
C
Love, Affection
D
Abundance, Scarcity
প্রশ্নের বিশ্লেষণ
-
False – মিথ্যা
-
True – সত্য
➡️ একে অপরের বিপরীতার্থক (Antonym)। -
Sharp – তীক্ষ্ণ
-
Blunt – ভোঁতা
➡️ এটিও বিপরীতার্থক (Antonym)। -
Love – ভালোবাসা
-
Affection – প্রেম
➡️ এখানে শব্দ দুটির অর্থ কাছাকাছি, অর্থাৎ সমার্থক (Synonym)। -
Abundance – প্রাচুর্য
-
Scarcity – ঘাটতি
➡️ একে অপরের বিপরীতার্থক (Antonym)।
উপসংহার: এখানে চারটি অপশনের মধ্যে কেবলমাত্র (গ) নম্বর অপশনটিতে Synonym (সমার্থক শব্দ) আছে। আর বাকি সবগুলোতে Antonym (বিপরীতার্থক শব্দ) দেওয়া হয়েছে। তাই ভিন্ন অপশন হলো (গ) – Love & Affection।
তথ্যসূত্র: Oxford Advanced Learner’s Dictionary, Cambridge English Dictionary.
0
Updated: 3 weeks ago
