যদি cotθ = 1 হয়, তবে sinθ - cos(- θ) = কত?
A
1
B
2
C
0
D
√2
উত্তরের বিবরণ
প্রশ্ন: যদি cotθ = 1 হয়, তবে sinθ
- cos(- θ) = কত?
সমাধান:
দেওয়া আছে,
cotθ = 1
⇒
cotθ = cot45°
∴
θ = 45
এখন,
sinθ - cos(- θ)
= sinθ - cosθ
= sin45 - cos45°
= (1/√2) - (1/√2)
= 0
0
Updated: 1 month ago
প্রশ্ন:
Created: 5 months ago
A
√7
B
3√7
C
4
D
4√7
প্রশ্ন:
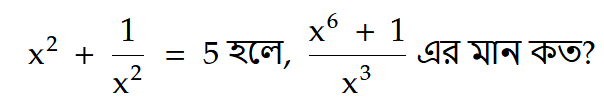
সমাধান:
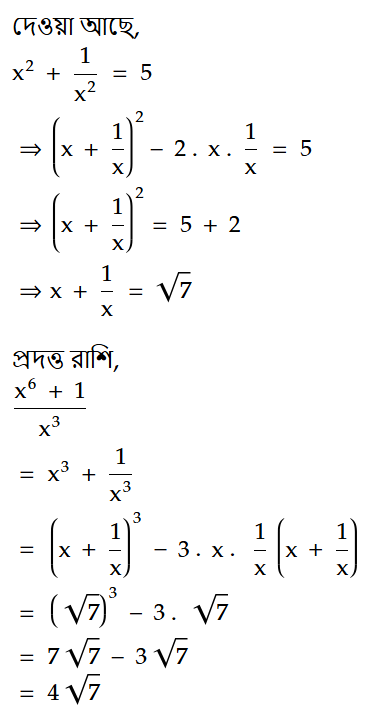
0
Updated: 5 months ago
What is the value of,
Created: 1 month ago
A
4
B
16
C
√10
D
√6
Question: What is the value of,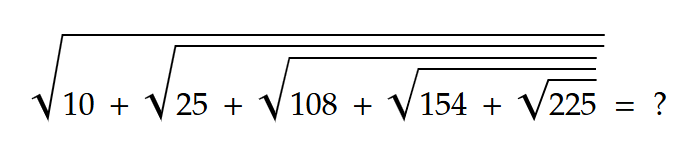
Solution: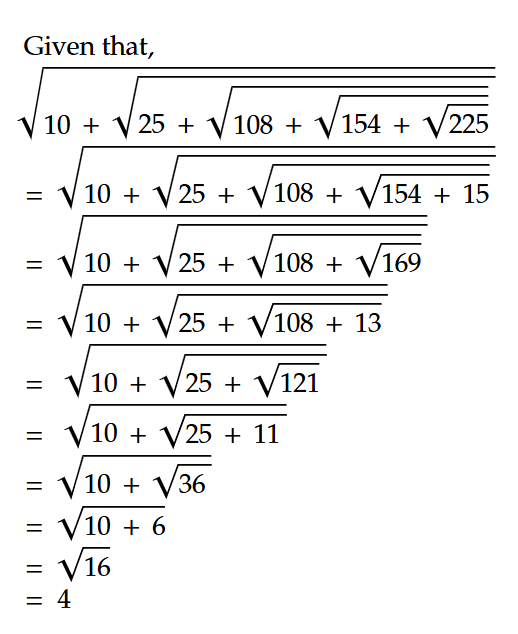
0
Updated: 1 month ago
Solve: x4 -
5x2 + 4 = 0
Created: 1 month ago
A
± 1, ± 5
B
± 3, ± 2
C
± 1, ± 2
D
± 4, ± 1
Question: Solve: x4 - 5x2 + 4 = 0
Solution:
Given,
x4 - 5x2 + 4 = 0
(x2)2 - 5x2 + 4 = 0
Let
x2 = a
∴ a2 - 5a + 4 = 0
⇒ a2 - 4a - a + 4 = 0
⇒ a(a - 4) - 1(a - 4) = 0
⇒ (a - 4)(a - 1) = 0
∴ a - 4 = 0
⇒ a = 4
⇒ x2 = 4
∴ x = ± 2
and,
a - 1 = 0
⇒ a = 1
⇒ x2 = 1
∴ x = ± 1
∴ x = ± 1, ± 2
0
Updated: 2 weeks ago