একটি 20 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 4 মিটার নিচে নেমে আসবে?
A
12 মিটার
B
13 মিটার
C
10 মিটার
D
16 মিটার
উত্তরের বিবরণ
প্রশ্ন: একটি 20 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 4 মিটার নিচে নেমে আসবে?
সমাধান: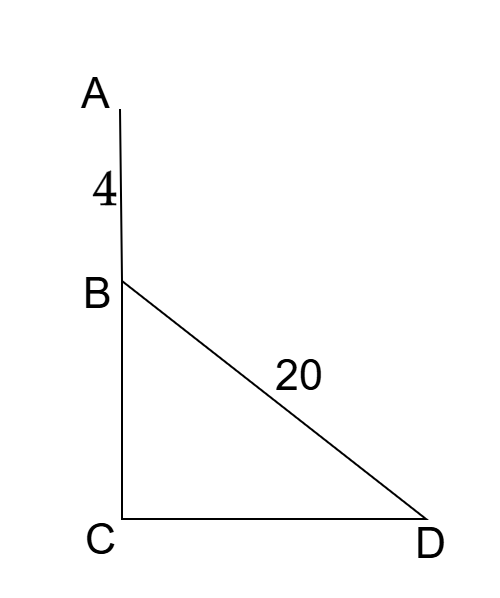
এখানে, AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত A বিন্দু থেকে B বিন্দুতে 4 মিটার নামবে। মইয়ের দৈর্ঘ্য, AC = BD = 20 মিটার
এবং AB = 4 মিটার, BC = 20 - 4 = 16 মিটার
এখন, পীথাগোরাসের সূত্র অনুযায়ী,
BC2 + CD2 = BD2
⇒ CD2 = BD2 - BC2
⇒ CD2 = 202 - 162
⇒ CD2 = 400 - 256
⇒ CD2 = 144
⇒ CD = √144
∴ CD = 12
∴ মইটির গোড়া দেয়াল থেকে 12 মিটার দূরে সরালে উপরের প্রান্ত 4 মিটার নিচে নামবে।
0
Updated: 1 month ago
x + y = 2 এবং x2 + y2 = 4 হলে, x3 + y3 = কত?
Created: 3 weeks ago
A
2
B
4
C
6
D
8
সমাধান:
আমরা জানি,
(x + y)2 = x2 + y2 + 2xy
বা, 22 = 4 + 2xy
বা, 4 = 4 + 2xy
বা, 2xy = 0
∴ xy = 0
প্রদত্ত রাশি,
x3 + y3 = (x + y)3 - 3xy(x + y)
= 23 - 3 × 0 × 2
= 8 - 0
= 8
আমরা জানি,
(x + y)2 = x2 + y2 + 2xy
বা, 22 = 4 + 2xy
বা, 4 = 4 + 2xy
বা, 2xy = 0
∴ xy = 0
প্রদত্ত রাশি,
x3 + y3 = (x + y)3 - 3xy(x + y)
= 23 - 3 × 0 × 2
= 8 - 0
= 8
0
Updated: 3 weeks ago
নিচের কোনটি মূলদ সংখ্যা?
Created: 2 weeks ago
A
∛243
B
∛343
C
∛392
D
∛676
0
Updated: 2 weeks ago
ছয়টি ক্রমিক স্বাভাবিক সংখ্যার প্রথম তিনটির যোগফল ২৪ হলে শেষ তিনটির যোগফল কত হবে?
Created: 2 months ago
A
২৭
B
৩০
C
৩৩
D
৩৬
প্রশ্ন: ছয়টি ক্রমিক স্বাভাবিক সংখ্যার প্রথম তিনটির যোগফল ২৪ হলে শেষ তিনটির যোগফল কত হবে?
সমাধান:
ধরি,
ছয়টি ক্রমিক স্বাভাবিক সংখ্যা যথাক্রমে ক, (ক + ১), (ক + ২), (ক + ৩), (ক + ৪), (ক + ৫)
প্রশ্নমতে,
ক + (ক + ১) + (ক + ২) = ২৪
⇒ ৩ক + ৩ = ২৪
⇒ ৩ক = ২৪ - ৩
⇒ ৩ক = ২১
⇒ ক = ২১/৩
⇒ ক = ৭
অর্থাৎ শেষ তিনটি সংখ্যা হবে, (৭ + ৩) = ১০,
(৭ + ৪) = ১১ এবং (৭ + ৫) = ১২
∴ শেষ তিনটি সংখ্যার যোগফল = ১০ + ১১ + ১২ = ৩৩
0
Updated: 2 months ago