পিতার বয়স পুত্রের বয়সের ৪ গুণ। ৫ বছর পর পিতার বয়স হবে পুত্রের বয়সের ৩ গুণ। পিতার বর্তমান বয়স কত?
A
৩০ বছর
B
৪০ বছর
C
৪৫ বছর
D
৬০ বছর
উত্তরের বিবরণ
প্রশ্ন: পিতার বয়স পুত্রের বয়সের ৪ গুণ। ৫ বছর পর পিতার বয়স হবে পুত্রের বয়সের ৩ গুণ। পিতার বর্তমান বয়স কত?
সমাধান:
ধরি, পুত্রের বর্তমান বয়স = ক বছর।
∴ পিতার বর্তমান বয়স = ৪ক বছর।
৫ বছর পরে,
পুত্রের বয়স = ক + ৫
পিতার বয়স = ৪ক + ৫
প্রশ্নমতে,
৪ক + ৫ = ৩(ক + ৫)
⇒ ৪ক + ৫ = ৩ক + ১৫
⇒ ৪ক - ৩ক = ১৫ - ৫
⇒ ক = ১০
∴ পিতার বর্তমান বয়স = ৪ × ১০ = ৪০ বছর
0
Updated: 1 month ago
সমীকরণটিতে p এর মান কত?
Created: 2 months ago
A
2/11
B
1
C
13/5
D
14/3
গণিত
অসমতা (Inequality)
বীজগণিত (Algebra)
সরল সমীকরণ (Simple/linear equation)
সরল-সহসমীকরণ (Simultaneous linear equations)
প্রশ্ন: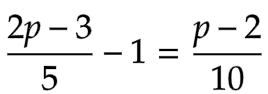 
সমীকরণটিতে p এর মান কত?
সমাধান: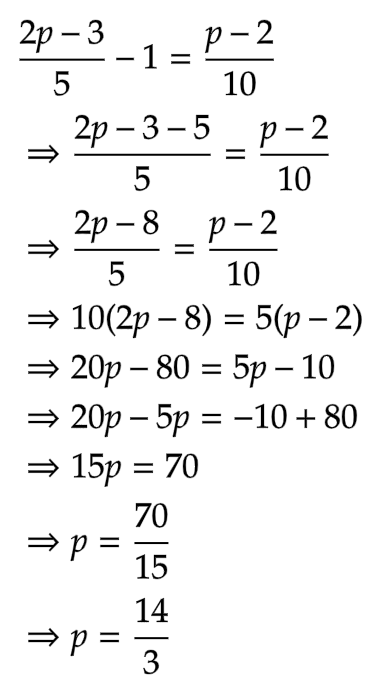
0
Updated: 2 months ago
log√8x = 10/3 হলে
x এর মান কত?
Created: 2 months ago
A
8
B
32
C
128
D
81
সমাধান:
দেওয়া আছে,
⇒ log√8x = 10/3
⇒ (√8)10/3 = x ;[logaN = x হলে, ax = N]
⇒ {√(23)}10/3 = x
⇒ (23/2)10/3 = x
⇒ 25 = x
⇒ x = 32
∴ x = 32
0
Updated: 2 months ago
যদি 3x2 - px + 27 = 0 সমীকরণের মূলদ্বয় সমান হয় এবং p < 0 হয় তাহলে p এর মান কত?
Created: 2 months ago
A
- 9
B
1/9
C
- 12
D
- 18
গণিত
অসমতা (Inequality)
বীজগণিত (Algebra)
সরল সমীকরণ (Simple/linear equation)
সরল-সহসমীকরণ (Simultaneous linear equations)
প্রশ্ন: যদি 3x2 - px + 27 = 0 সমীকরণের মূলদ্বয় সমান হয় এবং p < 0 হয় তাহলে p এর মান কত?
সমাধান:
প্রদত্ত সমীকরণটি হলো, 3x2 - px + 27 = 0
এই সমীকরণকে সাধারণ দ্বিঘাত সমীকরণ ax2 + bx + c = 0 এর সাথে তুলনা করে আমরা পাই,
a = 3, b = - p, এবং c = 27
আমরা জানি যে, একটি দ্বিঘাত সমীকরণের মূলদ্বয় সমান হওয়ার শর্ত হলো এর নিশ্চায়ক (discriminant) শূন্য হবে।
অর্থাৎ,b2 - 4ac = 0
⇒ (- p)2 - 4×3×27 = 0
⇒ p2 - 324 = 0
⇒ p2 = 324
⇒ p = ±√324
⇒ p = ±18
প্রশ্নে দেওয়া শর্ত অনুযায়ী, p < 0 হতে হবে।
সুতরাং, p-এর ঋণাত্মক মানটি গ্রহণ করতে হবে।
∴ p = - 18
0
Updated: 2 months ago
