প্রশ্ন: একটি শ্রেণিতে ২৫ জন ছাত্রের মধ্যে ১২ জন জীববিজ্ঞান এবং ৭ জন জীববিজ্ঞান ও উচ্চতর গণিত উভয় বিষয় নিয়েছে। ২ জন ছাত্র কোনো বিষয় নেয়নি। কতজন ছাত্র শুধু  উচ্চতর গণিত নিয়েছে?

সমাধান: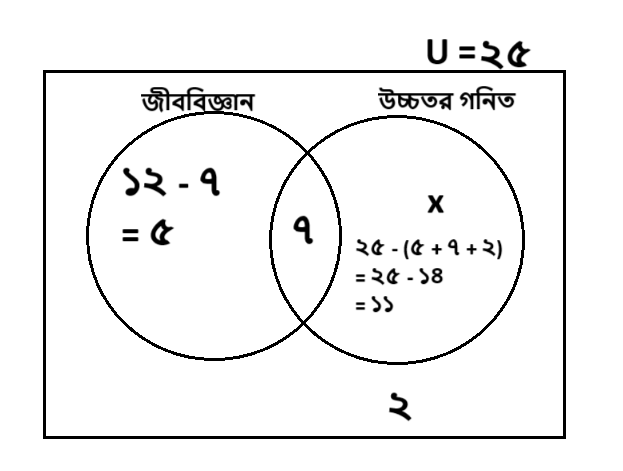

কোনো বিষয় নেয়নি = ২ জন 
উভয় বিষয় নিয়েছে = ৭ জন
শুধু জীববিজ্ঞান নিয়েছে = (১২ - ৭) জন = ৫ জন 
ধরি,
শুধু উচ্চতর গণিত নিয়েছে = x জন

প্রশ্নমতে,
৫ + x + ৭ + ২ = ২৫
⇒ ১৪ + x = ২৫
⇒ x = ২৫ - ১৪
⇒ x = ১১

অর্থাৎ ১১ জন ছাত্র শুধু উচ্চতর গণিত নিয়েছে। 

প্রশ্ন: ১ থেকে ১০০ পর্যন্ত ক্রমিক সংখ্যার গড় কত?

সমাধান:
ক্রমিক সংখ্যার গড় নির্ণয়ের সূত্র:
গড় = (প্রথম পদ + শেষ পদ)/২

এখানে, প্রথম পদ = ১, শেষ পদ = ১০০

অতএব, গড় = (১ + ১০০)/২
= ১০১/২
= ৫০.৫

∴ ১ থেকে ১০০ পর্যন্ত ক্রমিক সংখ্যার গড় হল ৫০.৫

Question: In a class, 30 students play basketball, 20 students play volleyball, and 8 students play both. 12 students play neither basketball nor volleyball. What is the total number of students in the class?

​​Solution:

Number of students who play basketball, n(B) = 30

Number of students who play volleyball, n(V) = 20

Number of students who play both basketball and volleyball, n(B ∩ V) = 8

Number of students who play neither = 12

n(B ∪ V) = n(B) + n(V) - n(B ∩ V)

= 30 + 20 - 8 = 42

Total students in the class = students who play basketball or volleyball + students who play neither

n(U) = n(B ∪ V) + neither = 42 + 12 = 54

∴ Total 54 students in the class.