প্রশ্ন: ১ থেকে ১০০ পর্যন্ত ক্রমিক সংখ্যার গড় কত?

সমাধান:
ক্রমিক সংখ্যার গড় নির্ণয়ের সূত্র:
গড় = (প্রথম পদ + শেষ পদ)/২

এখানে, প্রথম পদ = ১, শেষ পদ = ১০০

অতএব, গড় = (১ + ১০০)/২
= ১০১/২
= ৫০.৫

∴ ১ থেকে ১০০ পর্যন্ত ক্রমিক সংখ্যার গড় হল ৫০.৫

প্রশ্ন: একটি 20 মিটার লম্বা মই দেয়ালের সাথে খাড়া করে রাখা আছে। মইটির গোড়া দেয়াল থেকে কত দূরে সরালে এর উপরের অংশ 4 মিটার নিচে নেমে আসবে?

সমাধান: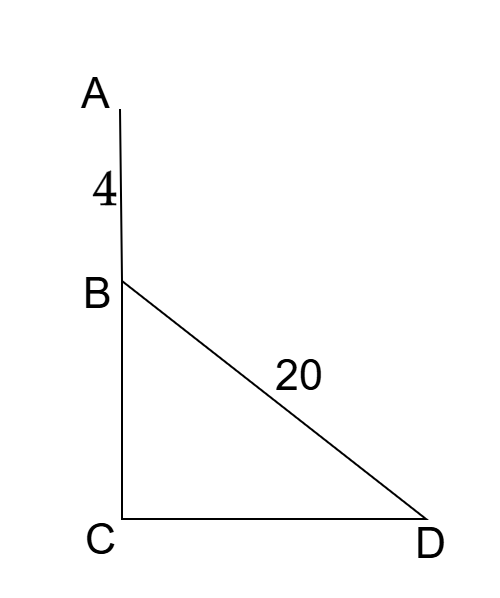


এখানে, AC মইয়ের গোড়া C থেকে D বিন্দুতে সরালে উপরের প্রান্ত A বিন্দু থেকে B বিন্দুতে 4 মিটার নামবে। মইয়ের দৈর্ঘ্য, AC = BD = 20 মিটার 
এবং AB = 4 মিটার, BC = 20 - 4 = 16 মিটার 

এখন, পীথাগোরাসের সূত্র অনুযায়ী,
BC2 + CD2 = BD2
⇒ CD2 = BD2 - BC2
⇒ CD2 = 202 - 162
⇒ CD2 = 400 - 256
⇒ CD2 = 144
⇒ CD = √144
∴ CD = 12

∴ মইটির গোড়া দেয়াল থেকে 12 মিটার দূরে সরালে উপরের প্রান্ত 4 মিটার নিচে নামবে।

প্রশ্ন: কোনো বৃত্তের ব্যাসার্ধ ৮ সে.মি. হলে ঐ বৃত্তের বৃহত্তম জ্যা এর দৈর্ঘ্য কত?

সমাধান:
আমরা জানি,
বৃত্তের বৃহত্তম জ্যা = বৃত্তের ব্যাস 
= ২ × ব্যাসার্ধ 
= (২ × ৮) সে.মি.
= ১৬ সে.মি.

• বৃত্তের কেন্দ্র দিয়ে অতিক্রমকারী জ্যা-কে ব্যাস বলে।
• কোনো বৃত্তের ব্যাস হলো তার বৃহত্তম জ্যা।
• ব্যাস হলো ব্যাসার্ধের দ্বিগুণ। অর্থাৎ, ব্যাস = ২ × ব্যাসার্ধ।