কোনটি অক্টাল সংখ্যা (24)8 এর সঠিক বাইনারি রূপ?
A
(111 100)2
B
(101 010)2
C
(111 101)2
D
(010 100)2
উত্তরের বিবরণ
অক্টাল সংখ্যা (24)8 এর সঠিক বাইনারি রূপ হচ্ছে : (010 100)2
অক্টাল থেকে বাইনারিতে রূপান্তর:
- যে সংখ্যা পদ্ধতিতে ৮টি অঙ্ক বা চিহ্ন ব্যবহার করা হয়, তাকে অক্টাল সংখ্যা পদ্ধতি বলে।
- অক্টাল থেকে বাইনারি সংখ্যায় রূপান্তরের ক্ষেত্রে প্রতিটি অক্টাল অংক কে তিন বিট বিশিষ্ট বাইনারি রূপান্তর করলে বাইনারি সংখ্যা পাওয়া যায়। যেমন-১ = ০০১২ = ০১০৩ = ০১১৪ = ১০০
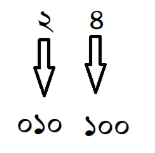
∴ (২৪)৮ = (010 100)2
উৎস: তথ্য ও যোগাযোগ প্রযুক্তি, একাদশ-দ্বাদশ শ্রেণি, উন্মুক্ত বিশ্ববিদ্যালয়।
অক্টাল থেকে বাইনারিতে রূপান্তর:
- যে সংখ্যা পদ্ধতিতে ৮টি অঙ্ক বা চিহ্ন ব্যবহার করা হয়, তাকে অক্টাল সংখ্যা পদ্ধতি বলে।
- অক্টাল থেকে বাইনারি সংখ্যায় রূপান্তরের ক্ষেত্রে প্রতিটি অক্টাল অংক কে তিন বিট বিশিষ্ট বাইনারি রূপান্তর করলে বাইনারি সংখ্যা পাওয়া যায়। যেমন-

∴ (২৪)৮ = (010 100)2
0
Updated: 1 month ago
নিচের কোনটি বাইনারি সংখ্যা পদ্ধতির বৈশিষ্ট্য নয়?
Created: 1 month ago
A
শুধু ০ ও ১ ব্যবহার করে
B
কম্পিউটারের মূল সংখ্যা পদ্ধতি
C
মানুষের দৈনন্দিন জীবনে সবচেয়ে বেশি ব্যবহৃত
D
ডিজিটাল ইলেকট্রনিক্সে ব্যবহৃত
বাইনারি সংখ্যা পদ্ধতি হলো একটি ভিত্তি-২ সংখ্যা পদ্ধতি, যেখানে শুধুমাত্র দুটি ডিজিট, ০ এবং ১, ব্যবহার করা হয়। এটি বিশেষভাবে কম্পিউটার এবং ডিজিটাল ইলেকট্রনিক্স-এর জন্য উপযোগী।
বাইনারি সংখ্যা পদ্ধতির মূল তথ্য:
-
এটি ২-ভিত্তিক সংখ্যা পদ্ধতি, যেখানে কেবল ০ এবং ১ ব্যবহার করা হয়।
-
এই দুটি অংককে বিভিন্নভাবে সাজিয়ে যেকোনো সংখ্যা প্রকাশ করা যায়।
-
বাইনারি পদ্ধতির বেজ হলো ২।
-
উদাহরণ: (110)₂, (1101)₂ ইত্যাদি।
-
কম্পিউটার বাইনারি সংখ্যার মাধ্যমে সমস্ত ডেটা সংরক্ষণ করে।
-
কম্পিউটারের অভ্যন্তরীণ প্রক্রিয়াকরণও বাইনারি সংখ্যা পদ্ধতিতে সম্পন্ন হয়।
উল্লেখ্য, মানুষের দৈনন্দিন জীবনে দশমিক (Decimal) সংখ্যা পদ্ধতি (০–৯) সবচেয়ে বেশি ব্যবহৃত হয়।
উৎস:
0
Updated: 1 month ago
কম্পিউটার কোন সংখ্যা পদ্ধতিতে কাজ করে?
Created: 2 months ago
A
রোমান
B
বাইনারি
C
দশমিক
D
ষোড়শিক
বাইনারি সংখ্যা পদ্ধতি:
- যে সংখ্যা পদ্ধতিতে সংখ্যা গণনা করার জন্য ২টি অঙ্ক বা প্রতীক ব্যবহৃত হয় তাকে বাইনারি সংখ্যা পদ্ধতি বলে।
যেমন-(১০১০)।
- বাইনারি সংখ্যা পদ্ধতিতে যেহেতু ০ এবং ১ এই দুইটি প্রতিক বা চিহ্ন ব্যবহার করা হয়।
- বাইনারি সংখ্যার ভিত্তি হচ্ছে ২।
- এ পদ্ধতিতে ০ এবং ১ মোট ২টি মৌলিক অঙ্ক আছে।
- বাইনারি সংখ্যার মাধ্যমে কম্পিউটারের সমস্ত যোগ বিয়োগ ও অন্যান্য কার্যাদি সম্পন্ন করা হয়।
উৎস: কম্পিউটার ও তথ্যপ্রযুক্তি-২, এসএসসি ও দাখিল (ভোকেশনাল)।
0
Updated: 2 months ago
(১২A)১৬ = (?)২
Created: 2 months ago
A
১০১০০১০১
B
১০০১০১০১০
C
১০০১০১০১০
D
১১০০১০০১
হেক্সাডেসিমাল → বাইনারি রূপান্তর
ধাপসমূহ:
-
হেক্সাডেসিমেল সংখ্যা লিখো।
-
প্রতিটি হেক্সাডেসিমেল অঙ্ককে ৪-বিট বাইনারি হিসেবে রূপান্তর করো:
-
সবগুলো মিলিয়ে লেখো:
উপসংহার:
উৎস:
তথ্য ও যোগাযোগ প্রযুক্তি, একাদশ ও দ্বাদশ শ্রেণি, প্রকৌশলী মুজিবুর রহমান
0
Updated: 2 months ago