x = (1/x) + (3/2) হলে, 8{x3 - (1/x3)} = কত?
A
63
B
62
C
61
D
60
উত্তরের বিবরণ
প্রশ্ন: x = (1/x) + (3/2) হলে, 8{x3 - (1/x3)} = কত?
সমাধান:
x = (1/x) + (3/2)
⇒ x - (1/x) = 3/2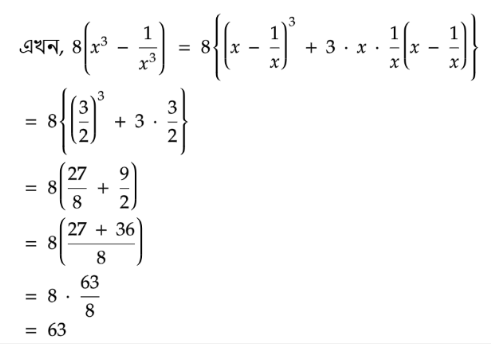
0
Updated: 1 month ago
যদি U = {1, 2, 3, 4, 5, 6, 7} এবং P = {2, 3, 5} এবং Q = {4, 6} হয়, তবে P ∩ Q' = কত?
Created: 2 months ago
A
P'
B
Ø
C
Q
D
P
গণিত
পরিসংখ্যান (Statistics)
বিন্যাস (Permutation)
বীজগণিত (Algebra)
সমাবেশ (Combination)
সম্ভাব্যতা (Probability)
সেট (Set)
প্রশ্ন: যদি U = {1, 2, 3, 4, 5, 6, 7} এবং P = {2, 3, 5} এবং Q = {4, 6} হয়, তবে P ∩ Q' = কত?
সমাধান:
দেওয়া আছে, U = {1, 2, 3, 4, 5, 6, 7}
P = {2, 3, 5} এবং Q = {4, 6}
এখন, Q' = U - Q = {1, 2, 3, 4, 5, 6, 7} - {4, 6}
= {1, 2, 3, 5, 7}
P ∩ Q' = {2, 3, 5} ∩ {1, 2, 3, 5, 7} = {2, 3, 5} = P
∴ P ∩ Q' = P
0
Updated: 2 months ago
সুদের হার দশমিক ৭৫ শতাংশ হ্রাস পাওয়াতে একজন আমানতকারীর উপর ৪ বছরের প্রাপ্ত আয় ৭৫০ টাকা কমে যায়। তার আমানতের মোট পরিমাণ কত?
Created: 3 days ago
A
২৫,০০০ টাকা
B
১৮,৭৫০ টাকা
C
৩০,০০০ টাকা
D
১,০০,০০০ টাকা
যখন দুটি সুদের হার থাকে এবং সুদের হার ও আয় কমে যায় তখন,
আসল = হ্রাসকৃত আয় x ১০০ / {(১ম সুদেরহার – ২য় সুদের হার) xসময়}
প্রশ্নে দেওয়া আছে,
হ্রাসকৃত আয় = ৭৫০
১ম সুদেরহার – ২য় সুদের হার = ০.৭৫
সময় = ৪
সুতরাং আসল = ৭৫০×১০০/(০.৭৫×৪) = ২৫,০০০
0
Updated: 3 days ago
x2 + px - 15 রাশিটির একটি উৎপাদক x + 5 হলে, p এর মান কত?
Created: 1 month ago
A
2
B
5
C
10
D
4
প্রশ্ন:
x2 + px - 15 রাশিটির
একটি উৎপাদক x + 5 হলে, p এর মান কত?
সমাধান:
ধরি, f(x) = x2 +
px - 15
x + 5, f(x) এর একটি উৎপাদক বলে
উৎপাদকের উপপাদ্য অনুযায়ী, f(- 5) = 0 হবে।
f(- 5) = (- 5)2 + p(- 5) - 15
= 25 - 5p - 15
= 10 - 5p
শর্তমতে,
10 - 5p = 0
⇒
10 = 5p
⇒
p = 10/5
⇒
p = 2
0
Updated: 1 month ago