Indignant শব্দটির সমার্থক হলো Angry।

• Indignant: রুষ্ট, ক্ষুদ্ধ

• Angry: রাগান্বিত, ক্রুদ্ধ, রুষ্ট

অর্থাৎ, উভয় শব্দই একই ধরনের রাগ বা ক্ষোভ প্রকাশ করে।

অন্যদিকে:

• Unskilled: অদক্ষ

• Improper: অনুচিত

• Money: টাকা

উৎস: 

প্রশ্ন: এক ব্যক্তি কোন স্থান থেকে যাত্রা শুরু করে দক্ষিণ দিকে 10 কি.মি. গেল। আবার সে পূর্ব দিকে 5 কি.মি.গেলো এবং গতি পরিবর্তন করে পুনরায় দক্ষিণ দিকে 7 কি.মি. গেলো এবং শেষে পশ্চিম দিকে 5কি.মি. গেলো। তার গন্তব্য স্থান ও যাত্রা স্থানের সরাসরি দূরত্ব কত?

সমাধান: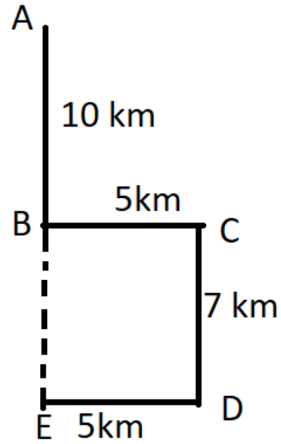

যাত্রাস্থান A এবং গন্তব্য স্থান E
সরাসরি দূরত্ব AE = (10 + 7) কি.মি. = 17 কি.মি.

প্রশ্ন: P বস্তু Q বস্তুর চেয়ে ভারি, R বস্তু S বস্তুর চেয়ে হালকা, P বস্তু R বস্তুর চেয়ে হালকা হলে, সবচেয়ে হালকা বস্তু কোনটি?

সমাধান:
P বস্তু Q বস্তুর চেয়ে ভারি, P > Q
R বস্তু S বস্তুর চেয়ে হালকা, S > R
P বস্তু R বস্তুর চেয়ে হালকা, R > P
সবগুলো সম্পর্ক থেকে পাই, Q < P < R < S
∴ সবচেয়ে হালকা বস্তু হবে Q.