একটি বালু ভর্তি ট্রাক A থেকে B পর্যন্ত যেতে ৩৯ কিমি/ঘণ্টায় যায় এবং খালি অবস্থায় B থেকে A অবস্থানে ফিরে আসতে ৫২ কিমি/ঘণ্টায় বেগে ফিরে আসে। ট্রাকটির গড় গতিবেগ কিমি/ঘণ্টা কত?
A
৪৪.৫৭ কিমি/ঘণ্টা
B
৪১.৫৬ কিমি/ঘণ্টা
C
৪০.৫৬ কিমি/ঘণ্টা
D
৩৮.৩৮কিমি/ঘণ্টা
উত্তরের বিবরণ
প্রশ্ন: একটি বালু ভর্তি ট্রাক A থেকে B পর্যন্ত যেতে ৩৯ কিমি/ঘন্টায় যায় এবং খালি অবস্থায় B থেকে A অবস্থানে ফিরে আসতে ৫২ কিমি/ঘন্টায় বেগে ফিরে আসে। ট্রাকটির গড় গতিবেগ কিমি/ঘণ্টা কত?
সমাধান:
দেওয়া আছে,
বালু ভর্তি অবস্থায় বেগ v1= ৩৯ কিমি/ঘণ্টা
খালি অবস্থায় বেগ v2= ৫২ কিমি/ঘণ্টা
গড় গতিবেগ = (২ × v1× v2)/(v1+ v2)
= (২ × ৩৯ × ৫২)/(৩৯ + ৫২ )
= ৪০৫৬ ÷ ৯১
= ৪৪.৫৭ কিমি/ঘণ্টা
0
Updated: 1 month ago
প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?
Created: 1 month ago
A
৬
B
৯
C
১১
D
১০
প্রশ্ন: প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?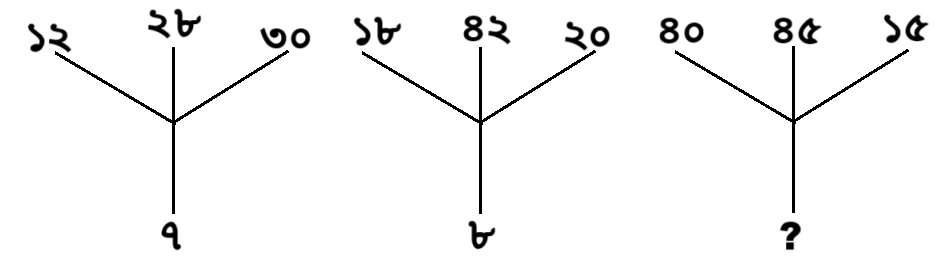
সমাধান:
উপরের তিনটি যোগফল ÷ ১০
১ম চিত্রে,
(১২ + ২৮ + ৩০) ÷ ১০
⇒ ৭০ ÷ ১০ = ৭
২য় চিত্রে,
(১৮ + ৪২ + ২০) ÷ ১০
⇒ ৮০ ÷ ১০ = ৮
৩য় চিত্রে,
(৪০ + ৪৫ + ১৫) ÷ ১০
⇒ ১০০ ÷ ১০ = ১০
সুতরাং, প্রশ্নবোধক স্থানে ১০ সংখ্যাটি বসবে।
0
Updated: 1 month ago
প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?
Created: 1 month ago
A
11
B
12
C
13
D
14
প্রশ্ন: প্রশ্নবোধক স্থানে কোন সংখ্যাটি বসবে?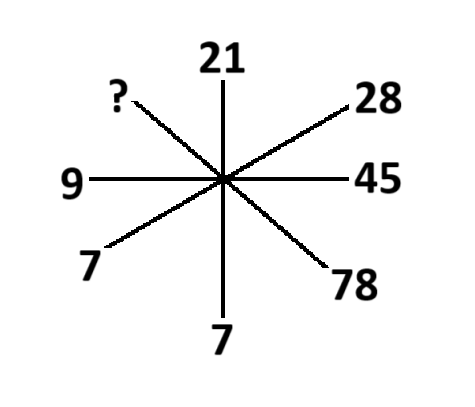
সমাধান:
নির্ণেয় সংখ্যা = 13
চিত্রটিতে,
7 × 3 = 21
7 × 4 = 28
9 × 5 = 45
13 × 6 = 78 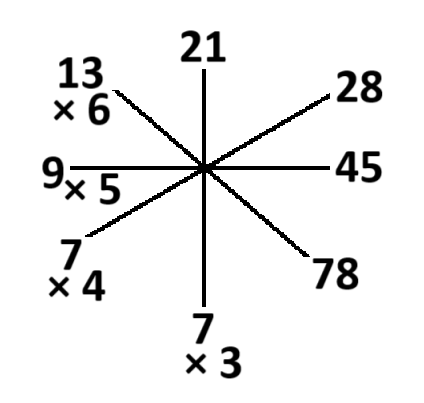
0
Updated: 1 month ago
নিচের কোন বানানটি শুদ্ধ?
Created: 1 month ago
A
শুশ্রুষা
B
সুশ্রুষা
C
শুশ্রূষা
D
শুস্রুশা
প্রদত্ত শব্দগুলোর মধ্যে শুদ্ধ বানান হলো শুশ্রূষা।
-
অর্থ: পরিচর্যা, সেবা
উৎস:
0
Updated: 1 month ago