যদি TABLE = ATELB হয়, তবে একই নিয়মে CHAIR = ?
A
CARIH
B
RICHA
C
HCRIA
D
HACIR
উত্তরের বিবরণ
প্রশ্ন: যদি TABLE = ATELB হয়, তবে একই নিয়মে CHAIR = ?
সমাধান:
TABLE = ATELB
এখানে,
১ম ও ২য় বর্ণ নিজেদের মাঝে স্থান পরিবর্তন করে।
৩য় ও ৫ম বর্ণ নিজেদের মাঝে স্থান পরিবর্তন করে।
৪র্থ বর্ণ নিজের স্থানেই থাকে।
CHAIR = HCRIA
একই ভাবে,
১ম ও ২য় বর্ণ নিজেদের মাঝে স্থান পরিবর্তন করে।
৩য় ও ৫ম বর্ণ নিজেদের মাঝে স্থান পরিবর্তন করে।
৪র্থ বর্ণ নিজের স্থানেই থাকে।
0
Updated: 1 month ago
যদি A পিস্টনে 8.8 N বল প্রয়োগ করা হয় তাহলে B পিস্টনে কত বল পাওয়া যাবে? (যেখানে A পিস্টনের ক্ষেত্রফল 5 বর্গমিটার এবং B পিস্টনের ক্ষেত্রফল 15 বর্গমিটার)
Created: 1 month ago
A
26.4 N
B
30 N
C
22.5 N
D
25 N
প্রশ্ন: যদি A পিস্টনে 8.8 N বল প্রয়োগ করা হয় তাহলে B পিস্টনে কত বল পাওয়া যাবে? (যেখানে A পিস্টনের ক্ষেত্রফল 5 বর্গমিটার এবং B পিস্টনের ক্ষেত্রফল 15 বর্গমিটার)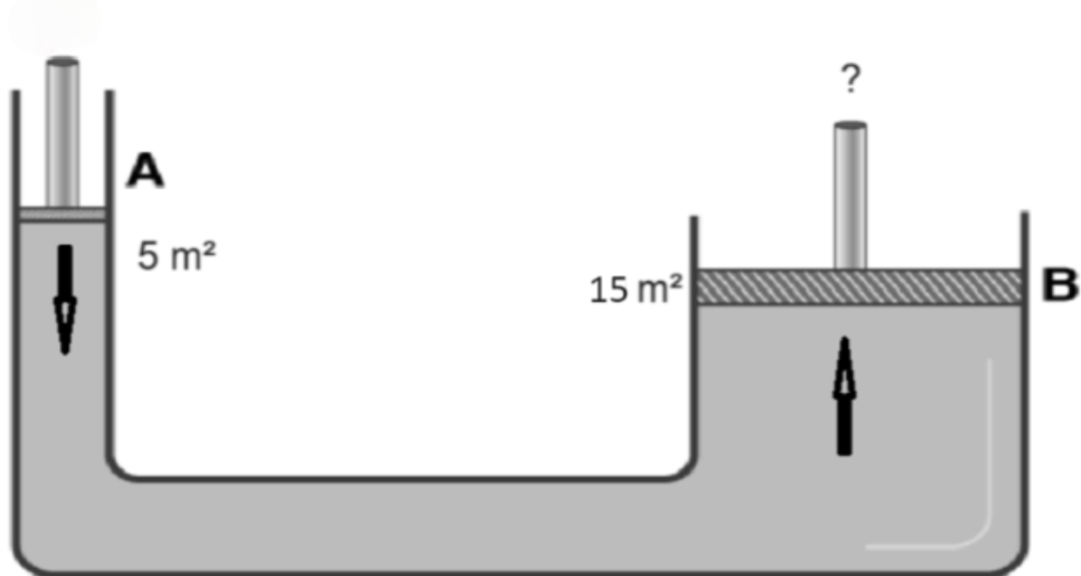
সমাধান:
প্যাসকেলের সূত্র হতে পাই,
F1/A1 = F2/A2
⇒ F2 = (F1 × A2)/A1 = (8.8 × 15)/5 = 26.4 N
0
Updated: 1 month ago
প্রশ্নবোধক চিহ্নিত স্থানে কোন সংখ্যা বসবে?
Created: 1 month ago
A
2
B
4
C
5
D
6
প্রশ্ন: প্রশ্নবোধক চিহ্নিত স্থানে কোন সংখ্যা বসবে?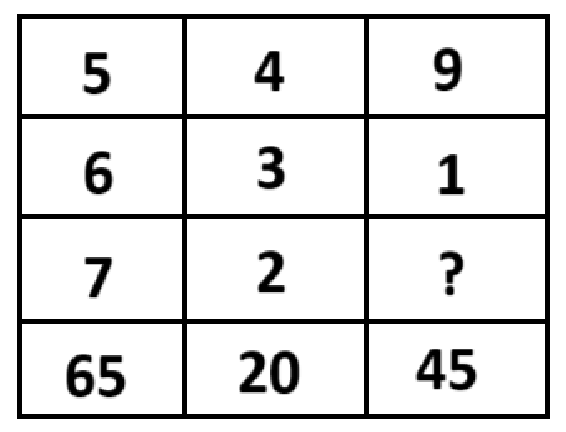
সমাধান:
নির্ণেয় সংখ্যাটি = 4
চিত্রের প্রথম কলামে,
5 × (6 + 7) = 5 × 13 = 65
দ্বিতীয় কলামে,
4 × (3 + 2) = 4 × 5 = 20
তৃতীয় কলামে,
ধরি, সংখ্যাটি = x
∴ 9 × (1 + x) = 45
⇒ 1 + x = 45/9 = 5
⇒ x = 5 - 1 = 4
0
Updated: 1 month ago
SUNFLOWER শব্দটির আয়নায় প্রতিবিম্ব কোনটি হবে?
Created: 1 month ago
A

B

C

D

প্রশ্ন: SUNFLOWER শব্দটির আয়নায় প্রতিবিম্ব কোনটি হবে?
সমাধান:
সঠিক উত্তর- ঘ) 
অর্থাৎ
0
Updated: 1 month ago