একটি গোলকের ব্যাস 12 সে.মি. হলে এর পৃষ্ঠের ক্ষেত্রফল কত?
A
144π বর্গ সে.মি.
B
120π বর্গ সে.মি.
C
124π বর্গ সে.মি.
D
100π বর্গ সে.মি.
উত্তরের বিবরণ
প্রশ্ন: একটি গোলকের ব্যাস 12 সে.মি. হলে এর পৃষ্ঠের ক্ষেত্রফল কত?
সমাধান:
দেওয়া আছে,
গোলকের ব্যাস, 2r = 12 সে.মি.
∴ গোলকের ব্যাসার্ধ, r = 12/2 সে.মি.
∴ r = 6 সে.মি.
আমরা জানি,
গোলকের পৃষ্ঠের ক্ষেত্রফল = 4πr2
= 4π(6)2
= 144π বর্গ সে.মি।
0
Updated: 1 month ago
18 ফুট উঁচু একটি খুঁটি এমনভাবে ভেঙ্গে গেল যে ভাঙ্গা অংশটি বিচ্ছিন্ন না হয়ে ভূমির সাথে 30° কোণে স্পর্শ করে, খুঁটিটি মাটি হতে কত ফুট উঁচুতে ভেঙ্গে ছিল?
Created: 1 month ago
A
3 ফুট
B
9 ফুট
C
6 ফুট
D
12 ফুট
প্রশ্ন: 18 ফুট উঁচু একটি খুঁটি এমনভাবে ভেঙ্গে গেল যে ভাঙ্গা অংশটি বিচ্ছিন্ন না হয়ে ভূমির সাথে 30° কোণে স্পর্শ করে, খুঁটিটি মাটি হতে কত ফুট উঁচুতে ভেঙ্গে ছিল?
সমাধান: 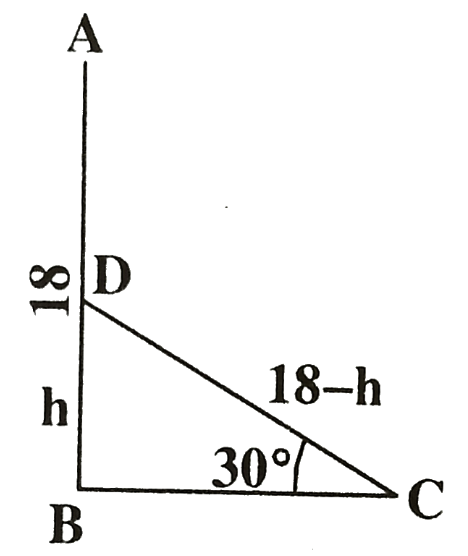
মনে করি,
খুঁটিটি মাটি হতে h ফুট উঁচুতে ভেঙ্গে ছিল।
∴ ভাঙ্গা অংশের দৈর্ঘ্য = (18 - h) ফুট
এখন,
Sinθ = লম্ব/অতিভুজ
বা, Sin30° = h/(18 - h)
বা, 1/2 = h/(18 - h)
বা, 18 - h = 2h
বা, 2h + h = 18
বা, 3h = 18
বা, h = 18/3
∴ h = 6
∴ খুঁটিটি মাটি হতে 6 ফুট উঁচুতে ভেঙ্গে ছিল।
0
Updated: 1 month ago
tanθ = 5/12 হলে, secθ - cosθ এর মান কত?
Created: 2 months ago
A
13/169
B
25/156
C
27/156
D
25/144
সমাধান:
দেওয়া আছে,
tanθ = 5/12
বা, লম্ব/ভূমি = 5/12
∴ অতিভুজ = √{(12)2 + (5)2}
= √(144 + 25)
= √169
= 13
প্রদত্ত রাশি = secθ - cosθ
= (অতিভুজ/ভূমি) - (ভূমি/অতিভুজ)
= (13/12) - (12/13)
= (169 - 144)/156
= 25/156
0
Updated: 2 months ago
(- 4, 5) এবং (1, 2) বিন্দুগামী একটি সরলরেখার ঢাল কত?
Created: 1 month ago
A
3/5
B
7/3
C
- 5/3
D
- 3/5
প্রশ্ন: (- 4, 5) এবং (1, 2) বিন্দুগামী একটি সরলরেখার ঢাল কত?
সমাধান:
আমরা জানি,
দুটি বিন্দু (x1, y1) এবং (x2, y2) দিয়ে অতিক্রমকারী একটি সরলরেখার ঢাল (m) নির্ণয়ের সূত্র হলো:
m = (y2 - y1)/(x2 - x1)
এখানে,
(x1, y1) = (- 4, 5) এবং (x2, y2) = (1, 2)
∴ ঢাল, (m) = (2 - 5)/{1 - (- 4)}
= - 3/(1 + 4)
= - 3/5
0
Updated: 1 month ago