2√2x3 + 125 এর সঠিক উৎপাদকের বিশ্লেষণ কোনটি?
A
(2x - 5)(x2 - 5√2x + 25)
B
(√3x + 5)(3x2 + 5√3x + 25)
C
(√2x + 5)(2x2 - 5√2x - 25)
D
(√2x + 5)(2x2 - 5√2x + 25)
উত্তরের বিবরণ
দেওয়া আছে,
2√2x3 + 125
= (√2x)3 + (5)3 ;[a3 + b3 = (a + b)(a2 - ab + b2)]
= (√2x + 5){(√2x)2 - √2x . 5 + 52}
= (√2x + 5)(2x2 - 5√2x + 25)
0
Updated: 1 month ago
যদি x = √5 + √3 হয়, তবে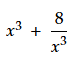 
এর মান কত?
Created: 1 month ago
A
18√5
B
22√5
C
28√5
D
32√5
প্রশ্ন: যদি x = √5 + √3 হয়, তবে 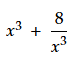এর মান কত?
সমাধান:
0
Updated: 1 month ago
একটি গুণোত্তর ধারার প্রথম ও দ্বিতীয় পদ যথাক্রমে 27 এবং 9, তাহলে ধারাটির দশম পদ কত?
Created: 1 month ago
A
1/3
B
1/525
C
1/729
D
1/615
প্রশ্ন: একটি গুণোত্তর ধারার প্রথম ও দ্বিতীয় পদ যথাক্রমে 27 এবং 9, তাহলে ধারাটির দশম পদ কত?
সমাধান:
দেওয়া আছে
ধারাটির প্রথম পদ, a = 27
ধারাটির দ্বিতীয় পদ, ar2 - 1 = ar = 9
অতএব সাধারণ অনুপাত, r = 9/27 = 1/3
আমরা জানি,
গুণোত্তর ধারার n তম পদ = arn - 1
∴ দশম পদ, ar10 - 1 = 27(1/3)9
= (33 × 1)/(33 × 36)
= 1/36
= 1/729
সুতরাং, ধারাটির দশম পদ 1/729
0
Updated: 1 month ago
Six bells commence tolling together and toll at intervals of 3, 5, 6, 9, 10, and 15 seconds respectively. In 45 minutes, how many times do they toll together?
Created: 1 month ago
A
19
B
30
C
31
D
34
Question: Six bells commence tolling together and toll at intervals of 3, 5, 6, 9, 10, and 15 seconds respectively. In 45 minutes, how many times do they toll together?
Solution:
3 = 31
5 = 51
6 = 2 × 3
9 = 32
10 = 2 × 5
15 = 3 × 5
∴ ল.সা.গু. = 21 × 32 × 51 = 2 × 9 × 5 = 90।
সুতরাং, ঘণ্টাগুলো প্রতি 90 সেকেন্ড পর পর একসাথে বাজবে।
এখন, 45 মিনিট = 45 × 60 = 2700 সেকেন্ড।
মোট 2700 সেকেন্ডে ঘণ্টাগুলো যতবার একসাথে বাজবে তার সংখ্যা হলো = 2700/90 = 30 বার।
যেহেতু ঘণ্টাগুলো প্রথমে একবার একসাথে বাজা শুরু করেছিল, তাই মোট সংখ্যাটি হবে 30 এর সাথে সেই প্রথমবারটি যোগ করে।
∴ মোট সংখ্যা = 30 + 1 = 31 বার।
সুতরাং, 45 মিনিটে ঘণ্টাগুলো মোট 31 বার একসাথে বাজবে।
0
Updated: 1 month ago
